【题目】设函数f(x)= ![]() ,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
A.p假q真
B.p假q假
C.p真q真
D.p真q假
参考答案:
【答案】C
【解析】解:作出函数f(x)= ![]() 的图象如图,
的图象如图,
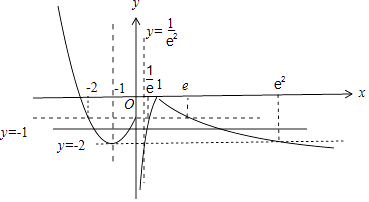
不妨设a<b<c<d,图中实线y=m与函数f(x)的图象相交于四个不同的点,由图可知m∈(﹣2,﹣1],
则a,b是x2+2x﹣m﹣1=0的两根,∴a+b=﹣2,ab=﹣m﹣1,
∴ab∈[0,1),且lnc=m,lnd=﹣m,
∴ln(cd)=0,
∴cd=1,
∴abcd∈[0,1),故①正确;
由图可知,c∈( ![]() ],
],
又∵cd=1,a+b=﹣2,
∴a+b+c+d=c+ ![]() ﹣2,在(
﹣2,在( ![]() ,
, ![]() ]是递减函数,
]是递减函数,
∴a+b+c+d∈[e+ ![]() ﹣2,e2+
﹣2,e2+ ![]() ﹣2),故②正确.
﹣2),故②正确.
∴p真q真.
所以答案是:C.
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
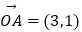 ,
, 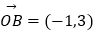 ,
, 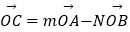 (m>0,n>0),若m+n∈[1,2],则
(m>0,n>0),若m+n∈[1,2],则 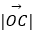 的取值范围是( )
的取值范围是( )
A.
B.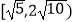
C.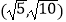
D.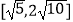
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=ex+mx2﹣m(m>0),当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( )
A.(﹣∞,0)
B.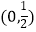
C.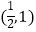
D.(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,角
中,角 的对边分别为
的对边分别为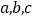 ,且
,且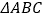 的面积
的面积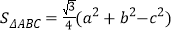 ,向量
,向量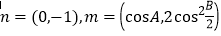 .
.(Ⅰ)求
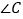 大小;
大小;(Ⅱ)求
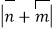 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数h(x)=ax3+bx2+cx+d(a≠0)图象的对称中心为M(x0 , h(x0)),记函数h(x)的导函数为g(x),则有g′(x0)=0,设函数f(x)=x3﹣3x2+2,则f(
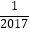 )+f(
)+f( 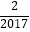 )+…+f(
)+…+f( 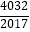 )+f(
)+f( 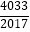 )= .
)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足
满足 ,且
,且 .
.(Ⅰ)证明:数列
 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;(Ⅱ)若记
 为满足不等式
为满足不等式 的正整数
的正整数 的个数,设
的个数,设 ,求数列
,求数列 的最大项与最小项的值.
的最大项与最小项的值.【答案】(1)见解析;(2)最大项为
 ,最小项为
,最小项为 .
.【解析】试题分析:(Ⅰ)对
 两边取倒数,移项即可得出
两边取倒数,移项即可得出 ,故而数列
,故而数列 为等差数列,利用等差数列的通项公式求出
为等差数列,利用等差数列的通项公式求出 ,从而可得出
,从而可得出 ;(Ⅱ)根据不等式
;(Ⅱ)根据不等式 ,,得
,,得 ,又
,又 ,从而
,从而 ,当
,当 为奇数时,
为奇数时, 单调递减,
单调递减, ;当
;当 为偶数时
为偶数时 单调递增,
单调递增, 综上
综上 的最大项为
的最大项为 ,最小项为
,最小项为 .
.试题解析:(Ⅰ)由于
 ,
, ,则
,则
∴
 ,则
,则 ,即
,即 为常数
为常数 又
 ,∴数列
,∴数列 是以1为首项,
是以1为首项, 为公比的等比数列
为公比的等比数列从而
 ,即
,即 .
.(Ⅱ)由
 即
即 ,得
,得 ,
,又
 ,从而
,从而
故

当
 为奇数时,
为奇数时, ,
, 单调递减,
单调递减, ;
;当
 为偶数时,
为偶数时, ,
, 单调递增,
单调递增,
综上
 的最大项为
的最大项为 ,最小项为
,最小项为 .
.【题型】解答题
【结束】
22【题目】已知向量
 ,
,
 ,若函数
,若函数 的最小正周期为
的最小正周期为 ,且在区间
,且在区间 上单调递减.
上单调递减.(Ⅰ)求
 的解析式;
的解析式;(Ⅱ)若关于
 的方程
的方程 在
在 有实数解,求
有实数解,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个内角A,B,C所对应的边分别为a,b,c,且满足bcosC+
 c=a.
c=a.
(1)求△ABC的内角B的大小;
(2)若△ABC的面积S=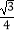 b2 , 试判断△ABC的形状.
b2 , 试判断△ABC的形状.
相关试题

