【题目】已知函数 其中
其中![]() 是实数.设
是实数.设![]() 为该函数图像上的两点,横坐标分别为
为该函数图像上的两点,横坐标分别为![]() ,且
,且![]() .
.
(1求![]() 的单调区间和极值;
的单调区间和极值;
(2)若![]() ,函数
,函数![]() 的图像在点
的图像在点![]() 处的切线互相垂直,求
处的切线互相垂直,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() 当
当![]() 时,
时,![]() 有极小值
有极小值![]() 无极大值;(2)
无极大值;(2)![]() 有最大值-1.
有最大值-1.
【解析】
试题分析:(1)先对函数![]() 求导,当导数大于0时单调递增,当导数小于0时单调递减,求方程
求导,当导数大于0时单调递增,当导数小于0时单调递减,求方程![]()
![]() 的根;、检查
的根;、检查![]() 与方程
与方程![]()
![]() 的根左右值的符号,如果左正右负,那么
的根左右值的符号,如果左正右负,那么![]() 在这个根处取得极大值,如果左负右正,那么
在这个根处取得极大值,如果左负右正,那么![]() 在这个根处取得极小值,(2)由
在这个根处取得极小值,(2)由![]() ,当
,当![]() 时,
时,![]() ,由函数
,由函数![]() 的图像在点
的图像在点![]() 处的切线互相垂直,由已知得
处的切线互相垂直,由已知得![]() ,可得
,可得![]() 的关系式,再利用基本不等式求出
的关系式,再利用基本不等式求出![]() 有最小值,即可得
有最小值,即可得![]() 有最大值
有最大值
试题解析:(1)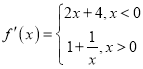
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
当![]() 时,
时,![]() 有极小值
有极小值![]() 无极大值.
无极大值.
(2)当![]() 时,
时,![]() ,
,
由已知得![]() ,
,
∴![]()
∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() ,当
,当![]() ,即
,即![]() 时,
时,![]() 有最小值1,即
有最小值1,即![]() 有最大值-1
有最大值-1
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次
赞成“留欧”
反对“留欧”
合计
18岁—19岁
6
50岁及50岁以上
10
合计
50
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据:
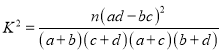 ,其中
,其中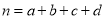
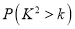
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
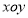 中,已知点
中,已知点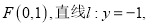
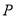 为平面上的动点,且过点
为平面上的动点,且过点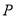 作
作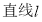 的垂线,垂足为
的垂线,垂足为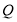 ,满足:
,满足: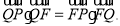
(Ⅰ)求动点
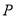 的轨迹
的轨迹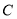 的方程;
的方程;(Ⅱ)在轨迹
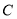 上求一点
上求一点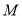 ,使得
,使得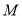 到直线
到直线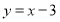 的距离最短,并求出最短距离.
的距离最短,并求出最短距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( ).
).(1)证明:直线
 过定点;
过定点;(2)若直线不经过第四象限,求
 的取值范围;
的取值范围;(3)若直线
 轴负半轴于
轴负半轴于 ,交
,交 轴正半轴于
轴正半轴于 ,△
,△ 的面积为
的面积为 (
( 为坐标原点),求
为坐标原点),求 的最小值,并求此时直线
的最小值,并求此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )

①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行
A.0 B.1 C.2 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
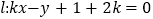 (
(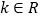 ).
).(1)证明:直线
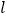 过定点;
过定点;(2)若直线不经过第四象限,求
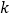 的取值范围;
的取值范围;(3)若直线
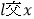 轴负半轴于
轴负半轴于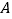 ,交
,交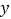 轴正半轴于
轴正半轴于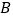 ,△
,△ 的面积为
的面积为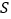 (
(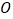 为坐标原点),求
为坐标原点),求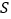 的最小值,并求此时直线
的最小值,并求此时直线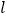 的方程.
的方程.
相关试题

