【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若对![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 在
在![]() 上的最大值.
上的最大值.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3) ![]()
【解析】试题分析:(1)将a=1代入求出函数的表达式,通过求导令导函数大于0,从而求出函数的单调递增区间;(2)问题转化为![]() 对1≤x≤e恒成立.记h(x)=
对1≤x≤e恒成立.记h(x)=![]() ,通过求导得到h(x)的单调性,从而求出a的范围;(3)先求出函数的导数,通过讨论当0<x<ln2k时,当ln2k<x<k时的情况,从而得到函数f(x)的最大值.
,通过求导得到h(x)的单调性,从而求出a的范围;(3)先求出函数的导数,通过讨论当0<x<ln2k时,当ln2k<x<k时的情况,从而得到函数f(x)的最大值.
试题解析:
⑴![]() 时,
时, ![]() ,
, ![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() .
.
所以函数![]() 的单调增区间为
的单调增区间为![]() .
.
⑵由题意 ![]() 对
对![]() 恒成立,因为
恒成立,因为![]() 时,
时, ![]() , 所以
, 所以![]() 对
对![]() 恒成立.记
恒成立.记![]() ,因为
,因为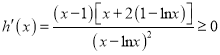 对
对![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,因此
,因此![]() .
.
⑶ 因为![]() ,由
,由![]() ,得
,得![]() 或
或![]() (舍).
(舍).
可证![]() 对任意
对任意![]() 恒成立,所以
恒成立,所以![]() ,
,
因为![]() ,所以
,所以![]() ,由于等号不能同时成立,所以
,由于等号不能同时成立,所以![]() ,于是
,于是![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调减函数;
上是单调减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数.
上是单调增函数.
所以![]() ,
,
记![]() ,
, ![]() ,以下证明当
,以下证明当![]() 时,
时, ![]() .
.
![]() ,记
,记![]() ,
, ![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调减函数,
上单调减函数, ![]() ,
, ![]() ,所以
,所以![]() ,使
,使![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数;当
上是单调增函数;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调减函数.又
上是单调减函数.又![]() ,所以
,所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,所以
恒成立,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x,y满足约束条件
 ,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+
,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+  )的图象向右平移
)的图象向右平移  后的表达式为( )
后的表达式为( )
A.y=tan(2x+ )
)
B.y=tan(x﹣ )
)
C.y=tan(2x﹣ )
)
D.y=tan2x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和是Sn,且Sn
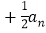 =1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=
=1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1= ,而b2,b5,ba14成等比数列.
,而b2,b5,ba14成等比数列.(1)求数列{an}、{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,∠BAC=90°,AB= AC = AA1=2,M,N分别是A1B1,BC的中点.

(1)证明:MN∥平面ACC1A1;
(2)求二面角M﹣AN﹣B的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=asinx
 cos2x+1(a,b∈R).
cos2x+1(a,b∈R).(1)当a=1,且

 时,求f(x)的值域;
时,求f(x)的值域;(2)若存在实数

 使得
使得 成立,求实数a的取值范围.
成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥S﹣ABC的各顶点都在一个半径为r的球面上,且SA=SB=SC=1,AB=BC=AC=
 ,则球的表面积为( )
,则球的表面积为( )A. 12π B. 8π C. 4π D. 3π
相关试题

