【题目】已知数列{an}的前n项和是Sn,且Sn![]() =1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=
=1(n∈N),数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() ,而b2,b5,ba14成等比数列.
,而b2,b5,ba14成等比数列.
(1)求数列{an}、{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】分析:(I)Sn![]() =1(n∈N),n≥2时,Sn﹣1+
=1(n∈N),n≥2时,Sn﹣1+![]() an﹣1=1,相减可得:an
an﹣1=1,相减可得:an![]() ﹣
﹣![]() an﹣1=0,化为:an=
an﹣1=0,化为:an=![]() an﹣1.利用等比数列的通项公式可得an.数列{bn}是公差d不等于0的等差数列,且满足:b1=
an﹣1.利用等比数列的通项公式可得an.数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() =1.由b2,b5,b14成等比数列.可得
=1.由b2,b5,b14成等比数列.可得![]() =b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)设cn=anbn=
=b2b14,(1+4d)2=(1+d)(1+13d),d≠0.解得d.即可得出;(Ⅱ)设cn=anbn=![]() ,利用错位相减法即可得出.
,利用错位相减法即可得出.
详解:
(1)Sn![]() =1(n∈N),n≥2时,Sn﹣1+
=1(n∈N),n≥2时,Sn﹣1+![]() an﹣1=1,相减可得:an
an﹣1=1,相减可得:an![]() ﹣
﹣![]() an﹣1=0,化为:an=
an﹣1=0,化为:an=![]() an﹣1.
an﹣1.
n=1时,a1+![]() =1,解得a1=
=1,解得a1=![]() .
.
∴数列{an}是等比数列,首项为![]() ,公比为
,公比为![]() .∴an=
.∴an=![]() =2×
=2×![]() .
.
数列{bn}是公差d不等于0的等差数列,且满足:b1=![]() =1.
=1.
∵b2,b5,b14成等比数列.∴![]() =b2b14,
=b2b14,
∴(1+4d)2=(1+d)(1+13d),d≠0.解得d=2.∴bn=1+2(n﹣1)=2n﹣1.
(2)设cn=anbn=![]() .
.
求数列{cn}的前n项和Tn=![]() +……+
+……+![]() .
.
![]() =
=![]() +……+
+……+![]() +
+![]() ,
,
相减可得:![]() Tn=
Tn=![]() +4
+4![]() ﹣
﹣![]() =
=![]() +4×
+4×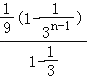 ﹣
﹣![]() ,
,
化为:Tn=2﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,圆
,圆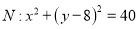 ,经过原点的两直线
,经过原点的两直线 满足
满足 ,且
,且 交圆
交圆 于不同两点交
于不同两点交 ,
,  圆
圆 于不同两点
于不同两点 ,记
,记 的斜率为
的斜率为
(1)求
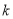 的取值范围;
的取值范围; (2)若四边形
 为梯形,求
为梯形,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x,y满足约束条件
 ,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+
,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+  )的图象向右平移
)的图象向右平移  后的表达式为( )
后的表达式为( )
A.y=tan(2x+ )
)
B.y=tan(x﹣ )
)
C.y=tan(2x﹣ )
)
D.y=tan2x -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
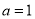 时,求
时,求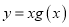 的单调区间;
的单调区间;(2)若对
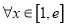 ,都有
,都有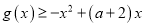 成立,求
成立,求 的取值范围;
的取值范围;(3)当
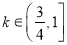 时,求
时,求 在
在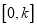 上的最大值.
上的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,∠BAC=90°,AB= AC = AA1=2,M,N分别是A1B1,BC的中点.

(1)证明:MN∥平面ACC1A1;
(2)求二面角M﹣AN﹣B的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=asinx
 cos2x+1(a,b∈R).
cos2x+1(a,b∈R).(1)当a=1,且

 时,求f(x)的值域;
时,求f(x)的值域;(2)若存在实数

 使得
使得 成立,求实数a的取值范围.
成立,求实数a的取值范围.
相关试题

