【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为x,求x的分布列和数学期望.
参考答案:
【答案】
(1)解:记事件 ![]() {从甲箱中摸出的1个球是红球},
{从甲箱中摸出的1个球是红球}, ![]() {从乙箱中摸出的1个球是红球}
{从乙箱中摸出的1个球是红球}
![]() {顾客抽奖1次获一等奖},
{顾客抽奖1次获一等奖}, ![]() {顾客抽奖1次获二等奖},
{顾客抽奖1次获二等奖}, ![]() {顾客抽奖1次能获奖},由题意,
{顾客抽奖1次能获奖},由题意, ![]() 与
与 ![]() 相互独立,
相互独立, ![]() 与
与 ![]() 互斥,
互斥, ![]() 与
与 ![]() 互斥,且
互斥,且 ![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
,
∵ ![]() ,
, ![]() ,∴
,∴ ![]() ,
,

![]() ,
,
故所求概率为 ![]()
(2)解:顾客抽奖3次独立重复试验,由(1)知,顾客抽奖1次获一等奖的概率为 ![]() ,∴
,∴ ![]() ,
,
于是 ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,故x的分布列为
,故x的分布列为
x | 0 | 1 | 2 | 3 |
p |
|
|
|
|
x的数学期望为 ![]() .
.
【解析】(1)顾客抽奖1次能获奖的情况有:顾客抽奖1次获一等奖,顾客抽奖1次获二等奖,分别求出两种情况的概率并相加即为所求;(2)顾客抽奖3次为独立重复试验,由(1)知,顾客抽奖1次获一等奖的概率为![]() ,根据n次独立重复实验中恰好发生k次的概率公式P(X=k)=
,根据n次独立重复实验中恰好发生k次的概率公式P(X=k)=![]() pk(1-p)n-k分别求出X所有可能取值的概率,列出分布列,根据服从二项分布的离散型随机变量的数学期望E(X)=np即可求解.
pk(1-p)n-k分别求出X所有可能取值的概率,列出分布列,根据服从二项分布的离散型随机变量的数学期望E(X)=np即可求解.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC

(1)求证:A,B,C,P四点共圆;
(2)若∠CAD= ,AB=1,求四边形ABCP的面积.
,AB=1,求四边形ABCP的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系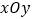 中,直线 的参数方程为
中,直线 的参数方程为  (
(  为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆  的极坐标方程为
的极坐标方程为  .
.
(1)写出圆 的直角坐标方程;
的直角坐标方程;
(2) 为直线
为直线  上一动点,当
上一动点,当  到圆心
到圆心  的距离最小时,求
的距离最小时,求  的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥
 中,侧面
中,侧面 与底面
与底面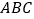 垂直,
垂直,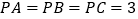 .
.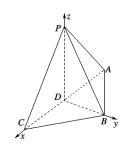
(1)求证:
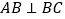 ;
;(2)设
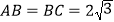 ,求
,求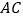 与平面
与平面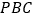 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设不经过坐标原点
 的直线
的直线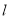 与圆
与圆 交于不同的两点
交于不同的两点 .若直线
.若直线 的斜率与直线
的斜率与直线 和
和 斜率满足
斜率满足 ,求
,求 面积
面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解关于
 的不等式
的不等式 ;
;(2)若
 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
相关试题

