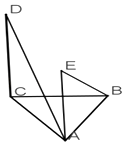
【题目】如图,在四棱锥P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点. 
(1)求证:平面PAB∥平面EFG;
(2)证明:平面EFG⊥平面PAD;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明.
参考答案:
【答案】
(1)证明:E,F分别是线段PC,PD的中点,所以EF∥CD,
又ABCD为正方形,AB∥CD,
所以EF∥AB,
又EF平面PAB,所以EF∥平面PAB.
因为E,G分别是线段PC,BC的中点,所以EG∥PB,
又EG平面PAB,所以,EG∥平面PAB.
所以平面EFG∥平面PAB
(2)证明:因为CD⊥AD,CD⊥PD,AD∩PD=D,所以CD⊥平面PAD,
又EF∥CD,所以EF⊥平面PAD,所以平面EFG⊥平面PAD
(3)证明:Q为线段PB中点时,PC⊥平面ADQ.
取PB中点Q,连接DE,EQ,AQ,
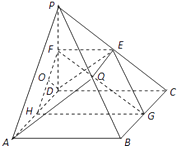
由于EQ∥BC∥AD,所以ADEQ为平面四边形,
由PD⊥平面ABCD,得AD⊥PD,
又AD⊥CD,PD∩CD=D,所以AD⊥平面PDC,
所以AD⊥PC,
又三角形PDC为等腰直角三角形,E为斜边中点,所以DE⊥PC,
AD∩DE=D,所以PC⊥平面ADQ.
【解析】(1)运用面面平行的判定定理,先证线面平行,即可得到证明;(2)由线面垂直的性质和面面垂直的判定定理,即可得证;(3)Q为线段PB中点时,PC⊥平面ADQ.运用线面垂直的判定定理即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
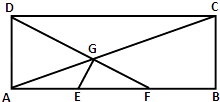
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G⊥D F. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且a1=0,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+log3n=log3bn , 求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
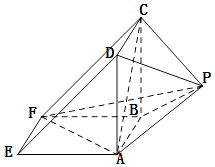
查看答案和解析>>【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2.
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是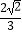 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.
(Ⅰ)若θ= ,且棱AB垂直于平面BCD,求四面体ABCD的体积;
,且棱AB垂直于平面BCD,求四面体ABCD的体积;
(Ⅱ)当θ= 时,证明:四面体ABCD的体积为一定值;
时,证明:四面体ABCD的体积为一定值;
(Ⅲ)求四面体ABCD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设α,β是两个不同的平面,m,n是两条不同的直线,有如下两个命题:q:若m⊥α,n⊥β且m∥n,则α∥β;q:若m∥α,n∥β且m∥n,则α∥β.( )
A.命题q,p都正确
B.命题p正确,命题q不正确
C.命题q,p都不正确
D.命题q不正确,命题p正确 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( )
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值
相关试题

