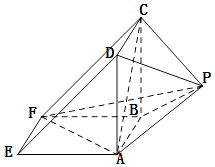
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2.
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
参考答案:
【答案】证明:(Ⅰ)∵几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,
∴AD⊥AF,AD⊥AB,
又AF∩AB=A,
∴AD⊥平面ABEF,
又AD平面PAD,
∴平面PAD⊥平面ABFE.
解:(Ⅱ)以A 为原点,AB、AE、AD的正方向为x,y,z轴,建立空间直角坐标系A﹣xyz
设正四棱棱的高为h,AE=AD=2,
则A(0,0,0),F(2,2,0),C(2,0,2),P(1,﹣1,1)
设平面ACF的一个法向量 ![]() =(x,y,z),
=(x,y,z),![]() =(2,2,0),
=(2,2,0), ![]() =(2,0,2),
=(2,0,2),
则 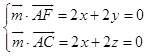 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,﹣1),
=(1,﹣1,﹣1),
设平面ACP的一个法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,取b=1,则
,取b=1,则 ![]() =(﹣1,1,1+h),
=(﹣1,1,1+h),
二面角C﹣AF﹣P的余弦值 ![]() ,
,
∴|cos< ![]() >|=
>|= ![]() =
= 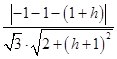 =
= ![]() ,
,
解得h=1.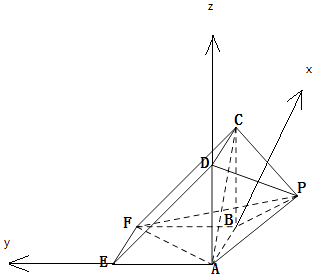
【解析】(Ⅰ)推导出AD⊥AF,AD⊥AB,从而AD⊥平面ABEF,由此能证明平面PAD⊥平面ABFE.(Ⅱ)以A 为原点,AB、AE、AD的正方向为x,y,z轴,建立空间直角坐标系A﹣xyz,利用向量法能求出h的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.F为PB中点.

(1)求证:EF∥面ABC;
(2)求证:EF⊥面PAC;
(3)求三棱锥B﹣PAC的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
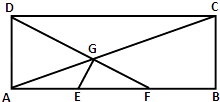
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G⊥D F. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且a1=0,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+log3n=log3bn , 求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.

(1)求证:平面PAB∥平面EFG;
(2)证明:平面EFG⊥平面PAD;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.
(Ⅰ)若θ= ,且棱AB垂直于平面BCD,求四面体ABCD的体积;
,且棱AB垂直于平面BCD,求四面体ABCD的体积;
(Ⅱ)当θ= 时,证明:四面体ABCD的体积为一定值;
时,证明:四面体ABCD的体积为一定值;
(Ⅲ)求四面体ABCD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设α,β是两个不同的平面,m,n是两条不同的直线,有如下两个命题:q:若m⊥α,n⊥β且m∥n,则α∥β;q:若m∥α,n∥β且m∥n,则α∥β.( )
A.命题q,p都正确
B.命题p正确,命题q不正确
C.命题q,p都不正确
D.命题q不正确,命题p正确
相关试题

