【题目】已知数列{an}的前n项和为Sn , 且a1=0,nan+1=Sn+n(n+1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足an+log3n=log3bn , 求数列{bn}的前n项和Tn .
参考答案:
【答案】解:(I)n≥2时,nan+1=Sn+n(n+1),(n﹣1)an=Sn﹣1+n(n﹣1).
相减可得:nan+1﹣(n﹣1)an=an+2n.
∴an+1﹣an=2.n=1时,a2=a1+2,∴a2﹣a1=2,
∴数列{an}为等差数列,an=0+2(n﹣1)=2n﹣2.
(II)∵数列{bn}满足an+log3n=log3bn ,
∴bn=32n﹣2×n
∴数列{bn}的前n项和Tn=1+2×9+3×92+…+n×9n﹣1 ,
∴9Tn=9+2×92+…+(n﹣1)×9n﹣1+n×9n ,
∴﹣8Tn=1+9+92+…+9n﹣1﹣n×9n= ![]() ﹣n×9n ,
﹣n×9n ,
可得:Tn= ![]()
【解析】(I)n≥2时,利用递推关系可得an+1﹣an=2.又a2﹣a1=2,数列{an}为等差数列,利用等差数列的通项公式即可得出.(II)数列{bn}满足an+log3n=log3bn , 可得bn=32n﹣2×n,再利用“错位相减法”与等比数列的求和公式即可得出.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系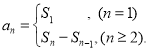 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,2,在Rt△ABC中,AB=BC=4,点E在线段AB上,过点E作交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°.
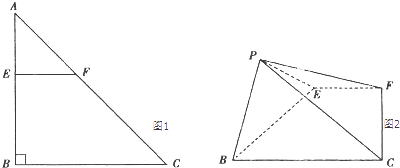
(1)求证:EF⊥PB;
(2)试问:当点E在何处时,四棱锥P﹣EFCB的侧面的面积最大?并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.F为PB中点.

(1)求证:EF∥面ABC;
(2)求证:EF⊥面PAC;
(3)求三棱锥B﹣PAC的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
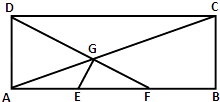
(1)若动点M到D点距离等于它到C点距离的两倍,求动点M的轨迹围成区域的面积;
(2)证明:E G⊥D F. -
科目: 来源: 题型:
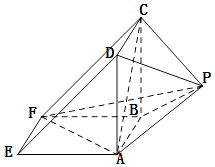
查看答案和解析>>【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2.
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是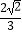 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.

(1)求证:平面PAB∥平面EFG;
(2)证明:平面EFG⊥平面PAD;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】四面体ABCD中,AB和CD为对棱.设AB=a,CD=b,且异面直线AB与CD间的距离为d,夹角为θ.
(Ⅰ)若θ= ,且棱AB垂直于平面BCD,求四面体ABCD的体积;
,且棱AB垂直于平面BCD,求四面体ABCD的体积;
(Ⅱ)当θ= 时,证明:四面体ABCD的体积为一定值;
时,证明:四面体ABCD的体积为一定值;
(Ⅲ)求四面体ABCD的体积.
相关试题

