【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() ,并且直线
,并且直线![]() 平分圆
平分圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在直线
两点,是否存在直线![]() ,使得
,使得![]() (
(![]() 为坐标原点),若存在,求出
为坐标原点),若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() ;(2) 不存在直线
;(2) 不存在直线![]() .
.
【解析】试题分析: (1)由弦的中垂线必过圆心,所以求出线段的中垂线,与3x-2y=0的交点即为圆心,由两点间距离公式求圆的半径.(2) 设![]() ,由向量的数量积坐标表示可知
,由向量的数量积坐标表示可知![]() ,直线与圆组方程组,利用韦达代入上式,可求得k,同时检验判别式.
,直线与圆组方程组,利用韦达代入上式,可求得k,同时检验判别式.
试题解析:(1)线段![]() 的中点
的中点![]() ,
,![]() ,
,
故线段![]() 的中垂线方程为
的中垂线方程为![]() ,即
,即![]() .
.
因为圆![]() 经过
经过![]() 两点,故圆心在线段
两点,故圆心在线段![]() 的中垂线上.
的中垂线上.
又因为直线![]() :
:![]() 平分圆
平分圆![]() ,所以直线
,所以直线![]() 经过圆心.
经过圆心.
由![]() 解得
解得![]() ,即圆心的坐标为
,即圆心的坐标为![]() ,
,
而圆的半径![]() ,
,
所以圆![]() 的方程为:
的方程为:![]()
(2)设![]() ,
,
将![]() 代入方程
代入方程![]() ,得
,得![]() ,
,
即![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,![]() .
.
又因为![]()
![]()
所以![]()
![]() ,解得
,解得![]() 或
或![]()
此时![]() 式中
式中![]() ,没有实根,与直线
,没有实根,与直线![]() 与
与![]() 交于
交于![]() 两点相矛盾,
两点相矛盾,
所以不存在直线![]() ,使得
,使得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】陕西省洛川地处北纬35°-36°,东经109°,昼夜温差
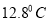 ,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用
,是国内外专家公认的世界最佳苹果优生区,是国家生态建设示范试点.近几年,果农为了提高经济效益,增加了广告和包装的投资费用,5年内果农投入的广告和包装费用 (万元)与销售额
(万元)与销售额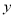 (万元)之间有下面对应数据:
(万元)之间有下面对应数据: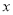
2
4
5
6
8
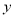
30
40
60
50
70
(1)假设
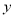 与
与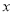 之间线性相关,求回归直线方程;
之间线性相关,求回归直线方程;(2)预测广告和包装费用为10(万元)时销售额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表和频率分布直方图,回答下面问题:
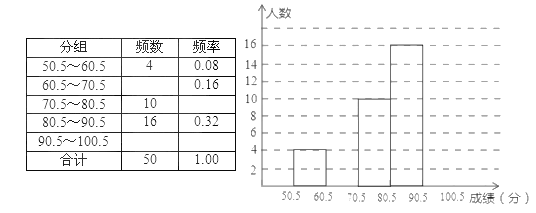
(1)结合图表信息,补全频率分布直方图;
(2)对于参加这次竞赛的900名学生,估计成绩不低于76分的约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
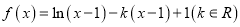 .
.(1)求函数
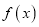 的单调区间;
的单调区间;(2)若
 满足:对任意的
满足:对任意的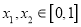 ,都有
,都有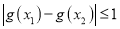 恒成立,试确定实数
恒成立,试确定实数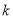 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
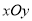 中,曲线
中,曲线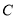 的参数方程为
的参数方程为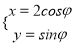 (
(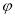 为参数),以坐标原点
为参数),以坐标原点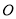 为极点,
为极点, 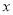 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线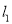 的极坐标方程为
的极坐标方程为 ,直线
,直线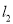 的极坐标方程为
的极坐标方程为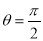 ,
, 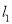 与
与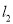 的交点为
的交点为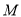 .
.(1)判断点
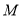 与曲线
与曲线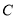 的位置关系;
的位置关系;(2)点
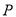 为曲线
为曲线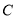 上的任意一点,求
上的任意一点,求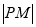 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知
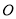 是边长为
是边长为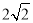 的正方形
的正方形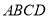 的中心,点
的中心,点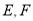 分别是
分别是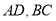 的中点,沿对角线
的中点,沿对角线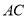 把正方形
把正方形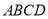 折成二面角
折成二面角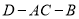 .
.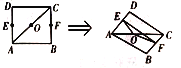
(1)证明:四面体
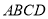 的外接球的体积为定值,并求出定值;
的外接球的体积为定值,并求出定值;(2)若二面角
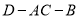 为直二面角,求二面角
为直二面角,求二面角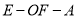 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.(1)求椭圆的标准方程;
(2)若直线
 与椭圆
与椭圆 相交于
相交于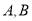 两点且
两点且 .求证:
.求证:  的面积为定值.
的面积为定值.
相关试题

