【题目】已知过抛物线![]() 的焦点,斜率为
的焦点,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线的方程;
(2) ![]() 为坐标原点,
为坐标原点,![]() 为抛物线上一点,若
为抛物线上一点,若![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)y2=8x.(2)λ=0,或λ=2.
【解析】试题分析:第一问求抛物线的焦点弦长问题可直接利用焦半径公式,先写出直线的方程,再与抛物线的方程联立方程组,设而不求,利用根与系数关系得出![]() ,然后利用焦半径公式得出焦点弦长公式
,然后利用焦半径公式得出焦点弦长公式![]() ,求出弦长,第二问根据联立方程组解出的A、B两点坐标,和向量的坐标关系表示出点C的坐标,由于点C在抛物线上满足抛物线方程,求出参数值.
,求出弦长,第二问根据联立方程组解出的A、B两点坐标,和向量的坐标关系表示出点C的坐标,由于点C在抛物线上满足抛物线方程,求出参数值.
试题解析:
(1)直线AB的方程是y=2![]() (x-2),与y2=8x联立,消去y得x2-5x+4=0,
(x-2),与y2=8x联立,消去y得x2-5x+4=0,
由根与系数的关系得x1+x2=5.由抛物线定义得|AB|=x1+x2+p=9,
(2)由x2-5x+4=0,得x1=1,x2=4,从而A(1,-2![]() ),B(4,4
),B(4,4![]() ).
).
设![]() =(x3,y3)=(1,-2
=(x3,y3)=(1,-2![]() )+λ(4,4
)+λ(4,4![]() )=(4λ+1,4
)=(4λ+1,4![]() λ-2
λ-2![]() ),
),
又y=8x3,即[2![]() (2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,
(2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,
解得λ=0或λ=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 ,椭圆
,椭圆 的长轴长是短轴长的2倍,
的长轴长是短轴长的2倍, 是椭圆
是椭圆 的右焦点,直线
的右焦点,直线 的斜率为
的斜率为 ,
, 为坐标原点.
为坐标原点.(1)求椭圆
 的方程;
的方程;(2)设过点
 的动直线
的动直线 与椭圆
与椭圆 相交于
相交于 两点.当
两点.当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=a(x-5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
 :
:  的左、右焦点分别为
的左、右焦点分别为 ,
,  ,
,  为椭圆上任一点,且
为椭圆上任一点,且 的最大值的取值范围是
的最大值的取值范围是 ,其中
,其中 ,则椭圆
,则椭圆 的离心率
的离心率 的取值范围是
的取值范围是A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 的边长为
的边长为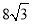 ,且其
,且其三个顶点均在抛物线
 上.
上.(Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)设动直线
 与抛物线
与抛物线 相切于点
相切于点 ,与直线
,与直线
相交于点
 .证明以
.证明以 为直径的圆恒过
为直径的圆恒过 轴上某定点.
轴上某定点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率
轴上,离心率 ,且椭圆
,且椭圆 经过点
经过点 ,过椭圆
,过椭圆 的左焦点
的左焦点 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆 于
于 ,
, 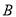 两点.
两点.(1)求椭圆
 的方程;
的方程;(2)设线段
 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点 ,求△
,求△ 的面积
的面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设双曲线
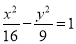 的左焦点为
的左焦点为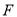 ,点
,点 为双曲线右支上的一点,且
为双曲线右支上的一点,且 与圆
与圆 相切于点
相切于点 为线段
为线段 的中点,
的中点,  为坐标原点,则
为坐标原点,则 __________.
__________.
相关试题

