【题目】已知函数f(x)=lnx+ax在点(t,f(t))处的切线方程为y=3x+1
(1)求a的值;
(2)已知k≤2,当x>1时,f(x)>k(1﹣ ![]() )+2x﹣1恒成立,求实数k的取值范围;
)+2x﹣1恒成立,求实数k的取值范围;
(3)对于在(0,1)中的任意一个常数b,是否存在正数x0 , 使得e ![]() +
+ ![]() x02<1?请说明理由.
x02<1?请说明理由.
参考答案:
【答案】
(1)解:函数f(x)=lnx+ax的导数为f′(x)= ![]() +a,
+a,
在点(t,f(t))处切线方程为y=3x+1,
可得f′(t)= ![]() +a,
+a,
∴函数的切线方程为y﹣(lnt+at)=( ![]() +a)(x﹣t),即y=(
+a)(x﹣t),即y=( ![]() +a)x+lnt﹣1,
+a)x+lnt﹣1,
∴ 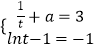 ,
,
解得a=2;
(2)证明:由(1)可得f(x)=lnx+2x,
∵f(x)>k(1﹣ ![]() )+2x﹣1,
)+2x﹣1,
∴lnx>k(1﹣ ![]() )﹣1
)﹣1
即为xlnx+x﹣k(x﹣3)>0,
可令g(x)=xlnx+x﹣k(x﹣3),
g′(x)=2+lnx﹣k,
由x>1,可得lnx>0,2﹣k≥0,
即有g′(x)>0,g(x)在(1,+∞)递增,
可得g(x)>g(1)=1+2k≥0,
∴﹣ ![]() ≤k≤2
≤k≤2
故k的取值范围为[﹣ ![]() ,2];
,2];
(3)解:对于在(0,1)中的任意一个常数b,
假设存在正数x0,使得:e ![]() +
+ ![]() x02<1.
x02<1.
由ef(x0+1)﹣3x0﹣2+ ![]() x02=eln(x0+1)﹣x0+
x02=eln(x0+1)﹣x0+ ![]() x02=(x0+1)e﹣x0+
x02=(x0+1)e﹣x0+ ![]() x02<1成立,
x02<1成立,
从而存在正数x0,使得上式成立,只需上式的最小值小于0即可.
令H(x)=(x+1)e﹣x+ ![]() x2﹣1,H′(x)=e﹣x﹣(x+1)e﹣x+bx=x(b﹣e﹣x),
x2﹣1,H′(x)=e﹣x﹣(x+1)e﹣x+bx=x(b﹣e﹣x),
令H′(x)>0,解得x>﹣lnb,令H′(x)<0,解得0<x<﹣lnb,
则x=﹣lnb为函数H(x)的极小值点,即为最小值点.
故H(x)的最小值为H(﹣lnb)=(﹣lnb+1)elnb+ ![]() ln2b﹣1=
ln2b﹣1= ![]() ln2b﹣blnb+b﹣1,
ln2b﹣blnb+b﹣1,
再令G(x)= ![]() ln2x﹣xlnx+x﹣1,(0<x<1),
ln2x﹣xlnx+x﹣1,(0<x<1),
G′(x)= ![]() (ln2x+2lnx)﹣(1+lnx)+1=ln2x>0,
(ln2x+2lnx)﹣(1+lnx)+1=ln2x>0,
则G(x)在(0,1)递增,可得G(x)<G(1)=0,则H(﹣lnb)<0.
故存在正数x0=﹣lnb,使得e ![]() +
+![]() x02<1.
x02<1.
【解析】(1)求出f(x)的导数,可得切线的斜率和切点,解方程可得a的值;(2)求出f(x)=lnx+x,要证原不等式成立,即证xlnx+x﹣k(x﹣3)>0,可令g(x)=xlnx+x﹣k(x﹣3),求出导数,判断符号,可得单调性,即可得证;(3)对于在(0,1)中的任意一个常数b,假设存在正数x0 , 使得e ![]() +
+ ![]() x02<1.运用转化思想可令H(x)=(x+1)e﹣x+
x02<1.运用转化思想可令H(x)=(x+1)e﹣x+ ![]() x2﹣1,求出导数判断单调性,可得最小值,即可得到结论
x2﹣1,求出导数判断单调性,可得最小值,即可得到结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4﹣4:坐标系与参数方程
在直角坐标xOy中,圆C1:x2+y2=4,圆C2:(x﹣2)2+y2=4.
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1 , C2的极坐标方程,并求出圆C1 , C2的交点坐标(用极坐标表示);
(2)求圆C1与C2的公共弦的参数方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.15),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65],并绘制出频率分布直方图,如图所示是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.

(1)求这次铅球投掷成绩合格的人数;
(2)你认为这次铅球投掷的同学的成绩的中位数在第几组?请说明理由;
(3)若参加这次铅球投掷的学生中,有5人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加相关部门组织的经验交流会,已知a、b 两位同学的成绩均为优秀,求a、b 两位同学中至少有1人被选到的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程)
已知曲线C1的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某百货公司1~6月份的销售量与利润的统计数据如表:
月份
1
2
3
4
5
6
销售量x/万件
10
11
13
12
8
6
利润y/万元
22
25
29
26
16
12
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程
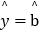 x+
x+ ;
;(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数的对称性有如下结论:对于给定的函数
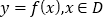 ,如果对于任意的
,如果对于任意的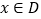 都有
都有 成立
成立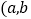 为常数),则函数
为常数),则函数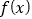 关于点
关于点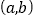 对称.
对称.(1)用题设中的结论证明:函数
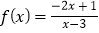 关于点
关于点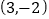 ;
;(2)若函数
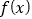 既关于点
既关于点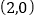 对称,又关于点
对称,又关于点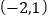 对称,且当
对称,且当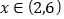 时,
时, ,求:①
,求:①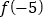 的值;
的值;②当
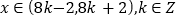 时,
时,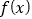 的表达式.
的表达式.
相关试题

