【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
参考答案:
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据题设中的结论证明即可;
(2)由题意可得![]() ,①代值计算即可;②由
,①代值计算即可;②由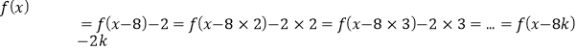 ,然后代值计算即可.
,然后代值计算即可.
(1)f(x)=![]() 的定义域为{x|x≠3},对任意x≠3有f(3﹣x)+f(3﹣x)=(﹣2﹣
的定义域为{x|x≠3},对任意x≠3有f(3﹣x)+f(3﹣x)=(﹣2﹣![]() )+(﹣2﹣
)+(﹣2﹣![]() )=﹣4,
)=﹣4,
∴函数f(x)=![]() 关于点(3,﹣2)对称;
关于点(3,﹣2)对称;
(2)函数f(x)关于点(2,0)对称,
∴f(2+x)+f(2﹣x)=0,
即f(x)+f(4﹣x)=0,
又关于点(﹣2,1)对称,
∴f(﹣2+x)+f(﹣2﹣x)=2,
即f(x)+f(﹣4﹣x)=2,
∴f(﹣4﹣x)=2+f(4﹣x),
即f(x+8)=f(x)﹣2,
①f(﹣5)=f(3)+2=23+3×3+2=19,
②x∈(8k﹣2,8k+2),x﹣8k∈(﹣2,2),4﹣(x﹣8k)∈(2,6),
∴f(x)=f(x﹣8)﹣2=f(x﹣8×2)﹣2×2=f(x﹣8×3)﹣2×3=…=f(x﹣8k)﹣2k,
又由f(t)=﹣f(4﹣t),
∴f(x)=f(x﹣8k)﹣2k=﹣f[4﹣(x﹣8k)]﹣2k=﹣[24﹣(x﹣8k)+3(4﹣(x﹣8k))]﹣2k,
∴即当x∈(8k﹣2,8k+2),k∈Z时,f(x)=﹣24﹣x+8k+3x﹣26k﹣12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx+ax在点(t,f(t))处的切线方程为y=3x+1
(1)求a的值;
(2)已知k≤2,当x>1时,f(x)>k(1﹣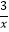 )+2x﹣1恒成立,求实数k的取值范围;
)+2x﹣1恒成立,求实数k的取值范围;
(3)对于在(0,1)中的任意一个常数b,是否存在正数x0 , 使得e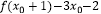 +
+  x02<1?请说明理由.
x02<1?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某百货公司1~6月份的销售量与利润的统计数据如表:
月份
1
2
3
4
5
6
销售量x/万件
10
11
13
12
8
6
利润y/万元
22
25
29
26
16
12
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程
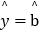 x+
x+ ;
;(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xoy中,曲线C1的参数方程为
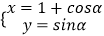 (α为参数),曲线C2的参数方程为
(α为参数),曲线C2的参数方程为  (β为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(β为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求曲线C1和曲线C2的极坐标方程;
(2)已知射线l1:θ=α( <α<
<α<  ),将射线l1顺时针方向旋转
),将射线l1顺时针方向旋转  得到l2:θ=α﹣
得到l2:θ=α﹣  ,且射线l1与曲线C1交于两点,射线l2与曲线C2交于O,Q两点,求|OP||OQ|的最大值.
,且射线l1与曲线C1交于两点,射线l2与曲线C2交于O,Q两点,求|OP||OQ|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校夏令营有3名男同学
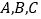 和3名女同学
和3名女同学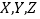 ,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
,其年级情况如下表,现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).一年级
二年级
三年级
男同学
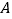
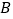
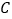
女同学
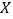
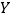
(1)用表中字母列举出所有可能的结果;
(2)设
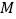 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件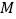 发生的概率.
发生的概率.
相关试题

