【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,
,![]() 是函数
是函数![]() 图象上任意不同的两点,线段
图象上任意不同的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .证明:
.证明:![]() .
.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)由条件可得![]() ,要求函数
,要求函数![]() 的单调区间,函数
的单调区间,函数![]() 的定义域为
的定义域为![]() 。求导得
。求导得![]() 。当
。当![]() 时,
时,![]() 。可得函数
。可得函数![]() 在
在![]() 上递增。(2)由函数
上递增。(2)由函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,可根据函数的单调性求函数的最小值,根据最小值等于
,可根据函数的单调性求函数的最小值,根据最小值等于![]() ,得到关于
,得到关于![]() 的关系式,即可求
的关系式,即可求![]() 。由(1)知
。由(1)知![]() 。因为
。因为![]() ,解不等式
,解不等式![]() ,
,![]() ,进而可得函数
,进而可得函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,进而可得
上递增,进而可得![]() ,所以
,所以![]() ,进而解得
,进而解得![]() 。满足
。满足![]() 。(3)要证明
。(3)要证明![]() ,应先把
,应先把![]() 和
和![]() 表示出来。由两点连线的斜率公式可得直线
表示出来。由两点连线的斜率公式可得直线![]() 的斜率为
的斜率为![]() ,由线段
,由线段![]() 的中点为
的中点为![]() ,可得
,可得![]() 。根据导函数可得
。根据导函数可得![]() 。所以要证
。所以要证![]() ,即证
,即证![]() 。以下利用分析法可证。不妨设
。以下利用分析法可证。不妨设![]() ,即证
,即证![]() ,即证
,即证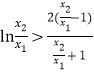 。把
。把![]() 看成整体。设
看成整体。设![]() ,即证
,即证![]() ,移项即证
,移项即证![]() ,其中
,其中![]() 。构造函数
。构造函数![]() 。证明函数的最小值大于0即可,求导数判断函数的单调性,进而求函数的最小值。
。证明函数的最小值大于0即可,求导数判断函数的单调性,进而求函数的最小值。
详解:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故函数![]() 在
在![]() 上递增。
上递增。
(2)由(1)知![]()
因为![]() ,
,
所以由![]() ,可得
,可得![]() ;
;
由![]() ,可得
,可得![]() 。
。
所以函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() 。
。
所以![]() ,
,
解得![]() ,符合题意。
,符合题意。
(3)证明:由已知可得![]()
又![]() ,所以
,所以![]() 。
。
要证![]() ,即证
,即证![]() 。
。
不妨设![]() ,即证
,即证![]() ,即证
,即证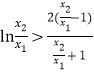 。
。
设![]() ,即证
,即证![]() ,
,
即证![]() ,其中
,其中![]() 。
。
设![]() ,
,
则![]()
所以![]() 在
在![]() 上单调递增,
上单调递增,
因此![]() 得证.
得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
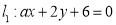 和
和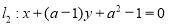 .
.(1)若
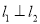 ,求实数
,求实数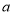 的值;
的值;(2)若
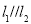 ,求实数
,求实数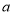 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
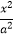 +
+ 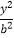 =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为  .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为  .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ,求直线AP的方程.
,求直线AP的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,
 )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设O为坐标原点,动点M在椭圆C:
 +y2=1上,过M做x轴的垂线,垂足为N,点P满足
+y2=1上,过M做x轴的垂线,垂足为N,点P满足  =
=  .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点Q在直线x=﹣3上,且
 =1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
=1.证明:过点P且垂直于OQ的直线l过C的左焦点F. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,椭圆E:
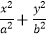 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 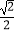 ,焦距为2.(14分)
,焦距为2.(14分)
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线l:y=k1x﹣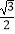 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2=
交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2= 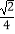 ,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.
,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.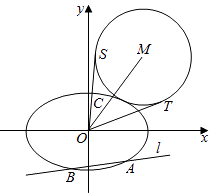
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:
①若
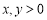 ,满足
,满足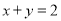 ,则
,则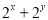 的最大值为
的最大值为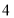 ;
;②若
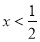 ,则函数
,则函数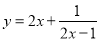 的最小值为
的最小值为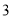
③若
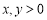 ,满足
,满足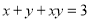 ,则
,则 的最小值为
的最小值为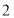
④函数
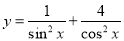 的最小值为
的最小值为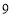
正确的有__________.(把你认为正确的序号全部写上)
相关试题

