【题目】已知抛物线C:y2=2px过点P(1,1).过点(0, ![]() )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
参考答案:
【答案】
(1)
解:(1)∵y2=2px过点P(1,1),
∴1=2p,
解得p= ![]() ,
,
∴y2=x,
∴焦点坐标为( ![]() ,0),准线为x=﹣
,0),准线为x=﹣ ![]() ,
,
(2)
(2)证明:设过点(0, ![]() )的直线方程为
)的直线方程为
y=kx+ ![]() ,M(x1,y1),N(x2,y2),
,M(x1,y1),N(x2,y2),
∴直线OP为y=x,直线ON为:y= ![]() x,
x,
由题意知A(x1,x1),B(x1, ![]() ),
),
由  ,可得k2x2+(k﹣1)x+
,可得k2x2+(k﹣1)x+ ![]() =0,
=0,
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]()
∴y1+ ![]() =kx1+
=kx1+ ![]() +
+ ![]() =2kx1+
=2kx1+ ![]() =2kx1+
=2kx1+  =
= ![]()
∴A为线段BM的中点.

【解析】(1.)根据抛物线过点P(1,1).代值求出p,即可求出抛物线C的方程,焦点坐标和准线方程;
(2.)设过点(0, ![]() )的直线方程为y=kx+
)的直线方程为y=kx+ ![]() ,M(x1 , y1),N(x2 , y2),根据韦达定理得到x1+x2=
,M(x1 , y1),N(x2 , y2),根据韦达定理得到x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,根据中点的定义即可证明.
,根据中点的定义即可证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 与
与 有表格中的数据,且
有表格中的数据,且 与
与 线性相关,由最小二乘法得
线性相关,由最小二乘法得 .
.
2
4
5
6
8

30
40
60
50
70
(1)求
 与
与 的线性回归方程;
的线性回归方程;(2)现有第二个线性模型:
 ,且
,且 .若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
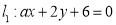 和
和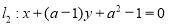 .
.(1)若
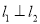 ,求实数
,求实数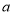 的值;
的值;(2)若
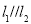 ,求实数
,求实数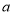 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
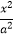 +
+ 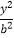 =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为  .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为  .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ,求直线AP的方程.
,求直线AP的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
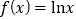 ,
,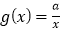 ,
,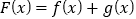 .
.(1)当
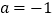 时,求函数
时,求函数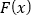 的单调区间;
的单调区间;(2)当
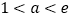 时,若函数
时,若函数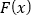 在区间
在区间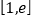 上的最小值是
上的最小值是 ,求
,求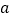 的值;
的值;(3)设
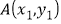 ,
, 是函数
是函数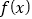 图象上任意不同的两点,线段
图象上任意不同的两点,线段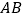 的中点为
的中点为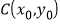 ,直线
,直线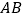 的斜率为
的斜率为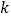 .证明:
.证明: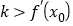 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设O为坐标原点,动点M在椭圆C:
 +y2=1上,过M做x轴的垂线,垂足为N,点P满足
+y2=1上,过M做x轴的垂线,垂足为N,点P满足  =
=  .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点Q在直线x=﹣3上,且
 =1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
=1.证明:过点P且垂直于OQ的直线l过C的左焦点F. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,椭圆E:
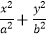 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 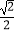 ,焦距为2.(14分)
,焦距为2.(14分)
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线l:y=k1x﹣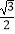 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2=
交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2= 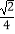 ,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.
,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.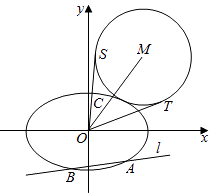
相关试题

