【题目】已知直线![]() 和
和![]() .
.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,求实数
,求实数![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)借助两直线垂直的充要条件建立方程求解;(2)借助两直线平行充要条件建立方程求解.
(1)若![]() ,则
,则![]() .
.
(2)若![]() ,则
,则![]() 或2.
或2.
经检验,![]() 时,
时,![]() 与
与![]() 重合,
重合,![]() 时,符合条件,∴
时,符合条件,∴![]() .
.
【点晴】
解析几何是运用代数的方法和知识解决几何问题一门学科,是数形结合的典范,也是高中数学的重要内容和高考的热点内容.解答本题时充分运用和借助题设条件中的垂直和平行条件,建立了含参数的直线的方程,然后再运用已知条件进行分析求解,从而将问题进行转化和化归,进而使问题获解.如本题的第一问中求参数![]() 的值时,是直接运用垂直的充要条件建立方程,这是方程思想的运用;再如第二问中求参数的值时也是运用了两直线平行的条件,但要注意的是这个条件不是两直线平行的充要条件,所以一定代回进行检验,这也是学生经常会出现错误的地方.
的值时,是直接运用垂直的充要条件建立方程,这是方程思想的运用;再如第二问中求参数的值时也是运用了两直线平行的条件,但要注意的是这个条件不是两直线平行的充要条件,所以一定代回进行检验,这也是学生经常会出现错误的地方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,且
,且 .
.(1)求
 的值及
的值及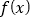 的定义域;
的定义域;(2)求
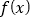 在区间
在区间 上的值域.
上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,双曲线
 =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 与
与 有表格中的数据,且
有表格中的数据,且 与
与 线性相关,由最小二乘法得
线性相关,由最小二乘法得 .
.
2
4
5
6
8

30
40
60
50
70
(1)求
 与
与 的线性回归方程;
的线性回归方程;(2)现有第二个线性模型:
 ,且
,且 .若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由
.若与(1)的线性模型比较,哪一个线性模型拟合效果比较好,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
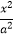 +
+ 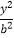 =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为  .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为  .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ,求直线AP的方程.
,求直线AP的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,
 )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(14分)
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
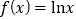 ,
,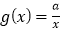 ,
,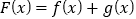 .
.(1)当
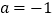 时,求函数
时,求函数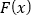 的单调区间;
的单调区间;(2)当
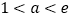 时,若函数
时,若函数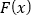 在区间
在区间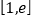 上的最小值是
上的最小值是 ,求
,求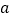 的值;
的值;(3)设
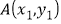 ,
, 是函数
是函数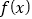 图象上任意不同的两点,线段
图象上任意不同的两点,线段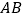 的中点为
的中点为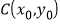 ,直线
,直线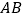 的斜率为
的斜率为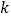 .证明:
.证明: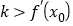 .
.
相关试题

