【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
③若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为
的最小值为![]()
④函数![]() 的最小值为
的最小值为![]()
正确的有__________.(把你认为正确的序号全部写上)
参考答案:
【答案】③④
【解析】
①令![]() ,得出
,得出![]() ,再利用双勾函数的单调性判断该命题的正误;
,再利用双勾函数的单调性判断该命题的正误;
②将函数解析式变形为![]() ,利用基本不等式判断该命题的正误;
,利用基本不等式判断该命题的正误;
③由![]() 得出
得出![]() ,得出
,得出![]() ,利用基本不等式可判断该命题的正误;
,利用基本不等式可判断该命题的正误;
④将代数式![]() 与代数式
与代数式![]() 相乘,展开后利用基本不等式可求出
相乘,展开后利用基本不等式可求出
![]() 的最小值,进而判断出该命题的正误。
的最小值,进而判断出该命题的正误。
①由![]() 得
得![]() ,则
,则![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,则
,则![]() ,则
,则![]() 上减函数,则
上减函数,则![]() 上为增函数,
上为增函数,
则![]() 时,
时,![]() 取得最小值
取得最小值![]() ,当
,当![]() 时,
时,![]() ,故
,故![]() 的最大值为
的最大值为![]() ,错误;
,错误;
②若![]() ,则函数
,则函数![]() ,
,
则![]()
![]() ,
,
即函数的最大值为![]() ,无最小值,故错误;
,无最小值,故错误;
③若![]() ,满足
,满足![]() ,则
,则![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,
,
则![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 得
得![]() ,即
,即![]() 时取等号,
时取等号,
即![]() 的最小值为
的最小值为![]() ,故③正确;
,故③正确;
④![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() ,即
,即![]() 时,取等号,
时,取等号,
即函数![]() 的最小值为
的最小值为![]() ,故④正确,故答案为:③④。
,故④正确,故答案为:③④。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
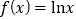 ,
,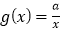 ,
,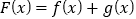 .
.(1)当
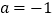 时,求函数
时,求函数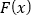 的单调区间;
的单调区间;(2)当
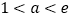 时,若函数
时,若函数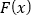 在区间
在区间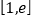 上的最小值是
上的最小值是 ,求
,求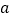 的值;
的值;(3)设
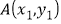 ,
, 是函数
是函数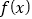 图象上任意不同的两点,线段
图象上任意不同的两点,线段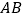 的中点为
的中点为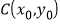 ,直线
,直线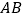 的斜率为
的斜率为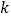 .证明:
.证明: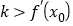 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设O为坐标原点,动点M在椭圆C:
 +y2=1上,过M做x轴的垂线,垂足为N,点P满足
+y2=1上,过M做x轴的垂线,垂足为N,点P满足  =
=  .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点Q在直线x=﹣3上,且
 =1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
=1.证明:过点P且垂直于OQ的直线l过C的左焦点F. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,椭圆E:
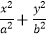 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 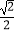 ,焦距为2.(14分)
,焦距为2.(14分)
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线l:y=k1x﹣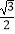 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2=
交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2= 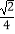 ,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.
,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.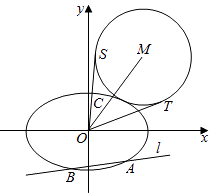
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线x2=y,点A(﹣
 ,
,  ),B(
),B(  ,
,  ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣  <x<
<x<  ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.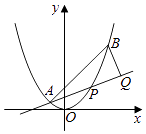
-
科目: 来源: 题型:
查看答案和解析>>【题目】微信是现代生活进行信息交流的重要工具,据统计,某公司
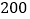 名员工中
名员工中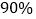 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有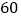 ,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于
,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于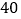 岁)和中年(年龄不小于
岁)和中年(年龄不小于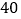 岁)两个阶段,那么使用微信的人中
岁)两个阶段,那么使用微信的人中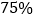 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中 是青年人.
是青年人.(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出
 列联表:
列联表:青年人
中年人
总计
经常使用微信
不经常使用微信
总计
(2)由列联表中所得数据判断,是否有百分之
 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?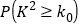
0.010
0.001

6.635
10.828
附:
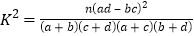
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,椭圆E:
 =1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为
=1(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为  ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1 , 过点F2作直线PF2的垂线l2 .
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1 , 过点F2作直线PF2的垂线l2 .
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线l1 , l2的交点Q在椭圆E上,求点P的坐标.
相关试题

