【题目】二次函数f(x)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
参考答案:
【答案】
(1)解:设f(x)=ax2+bx+c,由f(0)=1得c=1,故f(x)=ax2+bx+1.
因为f(x+1)﹣f(x)=2x,所以a(x+1)2+b(x+1)+1﹣(ax2+bx+1)=2x.
即2ax+a+b=2x,所以 ![]() ,∴
,∴ ![]() ,
,
所以f(x)=x2﹣x+1
(2)解:由题意得x2﹣x+1>2x+m在[﹣1,1]上恒成立.即x2﹣3x+1﹣m>0在[﹣1,1]上恒成立.
设g(x)=x2﹣3x+1﹣m,其图象的对称轴为直线 ![]() ,所以g(x)在[﹣1,1]上递减.
,所以g(x)在[﹣1,1]上递减.
故只需最小值g(1)>0,即12﹣3×1+1﹣m>0,
解得m<﹣1
【解析】(1)先设f(x)=ax2+bx+c,在利用f(0)=1求c,再利用两方程相等对应项系数相等求a,b即可.(2)转化为x2﹣3x+1﹣m>0在[﹣1,1]上恒成立问题,找其在[﹣1,1]上的最小值让其大于0即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在
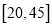 的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.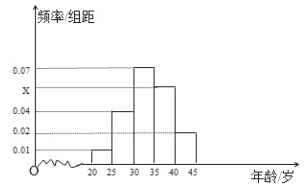
(Ⅰ)求图中
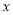 的值;
的值;(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为
 ,求
,求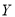 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O:x2+y2=16及圆内一点F(﹣3,0),过F任作一条弦AB.
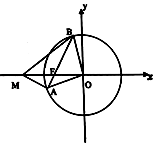
(1)求△AOB面积的最大值及取得最大值时直线AB的方程;
(2)若点M在x轴上,且使得MF为△AMB的一条内角平方线,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|﹣1<x<2},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中, ,
, ,
, ,
, ,
, 分别为
分别为 的中点,
的中点, .
.
(1)求证:平面
 平面
平面 ;
;(2)设
 ,若平面
,若平面 与平面
与平面 所成锐二面角
所成锐二面角 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
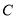 :
: 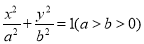 的离心率为
的离心率为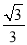 ,过右焦点
,过右焦点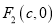 垂直于
垂直于 轴的直线与椭圆交于
轴的直线与椭圆交于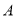 ,
,  两点且
两点且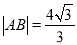 ,又过左焦点
,又过左焦点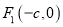 任作直线
任作直线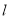 交椭圆于点
交椭圆于点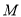 .
.(Ⅰ)求椭圆
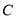 的方程;
的方程;(Ⅱ)椭圆
 上两点
上两点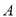 ,
, 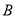 关于直线
关于直线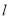 对称,求
对称,求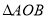 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=(ax﹣1)(x﹣1).
(1)若不等式f(x)<0的解集为{x|1<x<2},求实数a的值;
(2)当a>0时,解关于x的不等式f(x)<0.
相关试题

