【题目】设数列{an}的前n项和为Sn , 满足Sn=2nan+1﹣3n2﹣4n,n∈N* , 且S3=15.
(1)求a1 , a2 , a3的值;
(2)求数列{an}的通项公式.
参考答案:
【答案】
(1)
解:由Sn=2nan+1﹣3n2﹣4n,n∈N*,得:
S2=4a3﹣20 ①
又S3=S2+a3=15 ②
联立①②解得:a3=7.
再在Sn=2nan+1﹣3n2﹣4n中取n=1,得:
a1=2a2﹣7 ③
又S3=a1+a2+7=15 ④
联立③④得:a2=5,a1=3.
∴a1,a2,a3的值分别为3,5,7
(2)
解:∵a1=3=2×1+1,a2=5=2×2+1,a3=7=2×3+1.
由此猜测an=2n+1.
下面由数学归纳法证明:
①当n=1时,a1=3=2×1+1成立.
②假设n=k时结论成立,即ak=2k+1.
那么,当n=k+1时,
由Sn=2nan+1﹣3n2﹣4n,得 ![]() ,
,
![]() ,
,
两式作差得: ![]() .
.
∴ ![]()
= ![]() =2(k+1)+1.
=2(k+1)+1.
综上,当n=k+1时结论成立.
∴an=2n+1.
【解析】(1)在数列递推式中取n=2得一关系式,再把S3变为S2+a3得另一关系式,联立可求a3 , 然后把递推式中n取1,再结合S3=15联立方程组求得a1 , a2;(2)由(1)中求得的a1 , a2 , a3的值猜测出数列的一个通项公式,然后利用数学归纳法证明.
【考点精析】关于本题考查的数列的通项公式,需要了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随机观测生产某种零件的某工作厂25名工人的日加工零件个数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如下:
分组
频数
频率
[25,30]
3
0.12
(30,35]
5
0.20
(35,40]
8
0.32
(40,45]
n1
f1
(45,50]
n2
f2
(1)确定样本频率分布表中n1 , n2 , f1和f2的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
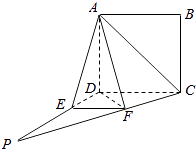
(1)证明:CF⊥平面ADF;
(2)求二面角D﹣AF﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
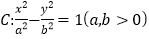 的离心率为
的离心率为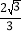 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.(1)求双曲线C的方程;
(2)直线y=kx+m(k≠0, m≠0)与该双曲线C交于不同的两点C,D,且C,D两点都在以点A为圆心的同一圆上,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 +
+  =1(a>b>0)的右焦点为(
=1(a>b>0)的右焦点为(  ,0),离心率为
,0),离心率为  .
.
(1)求椭圆C的标准方程;
(2)若动点P(x0 , y0)为椭圆C外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式
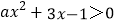 的解集是,
的解集是,
(1)求a的值;
(2)求不等式
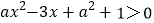 的解集.
的解集.
相关试题

