【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
参考答案:
【答案】
(1)解:设x<0,则﹣x>0,f(﹣x)=﹣(﹣x)2+2(﹣x)=﹣x2﹣2x.
又f(x)为奇函数,所以f(﹣x)=﹣f(x)且f(0)=0.
于是x<0时f(x)=x2+2x.
所以f(x)= ![]() .
.
(2)解:作出函数f(x)= ![]() 的图象如图:
的图象如图:
则由图象可知函数的单调递增区间为[﹣1,1]
要使f(x)在[﹣1,a﹣2]上单调递增,
结合f(x)的图象知 ![]() ,
,
所以1<a≤3,故实数a的取值范围是(1,3].
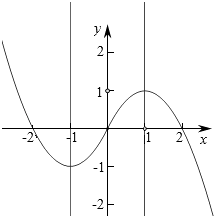
【解析】(1)根据函数奇偶性的对称性,即可求函数f(x)在R上的解析式;(2)根据函数奇偶性和单调性的关系,利用数形结合即可求出a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点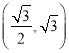 ,离心率为
,离心率为 .
.(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线
 交抛物线
交抛物线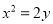 于
于 两点,
两点,  为原点.
为原点.①求证:
 ;
;②设
 、
、 分别与椭圆相交于
分别与椭圆相交于 、
、 两点,过原点
两点,过原点 作直线
作直线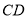 的垂线
的垂线 ,垂足为
,垂足为 ,证明:
,证明:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为坐标原点,
为坐标原点, 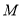 是椭圆
是椭圆 上的点,设动点
上的点,设动点 满足
满足 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)若直线
 与曲线
与曲线 相交于
相交于 ,
,  两个不同点,求
两个不同点,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】中心在原点,焦点在x轴上的一椭圆与一双曲线有共同的焦点F1,F2,且|F1F2|=
 ,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7.
,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7. (1)求这两曲线的方程;
(2)若P为这两曲线的一个交点,求cos∠F1PF2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,已知曲线
中,已知曲线 的参数方程为
的参数方程为 (
( 为参数),以直角坐标系原点
为参数),以直角坐标系原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的普通方程与直线
的普通方程与直线 的直角坐标方程;
的直角坐标方程;(Ⅱ)设点
 为曲线
为曲线 上的动点,求点
上的动点,求点 到直线
到直线 距离的最大值及其对应的点
距离的最大值及其对应的点 的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x),对任意a,b∈R,都有f(a+b)=f(a)+f(b)﹣1,当x>0时,f(x)>1;且f(2)=3,
(1)求f(0)及f(1)的值;
(2)判断函数f(x)在R上的单调性,并给予证明;
(3)若f(﹣kx2)+f(kx﹣2)<2对任意的x∈R恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
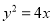 的焦点为
的焦点为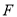 ,直线
,直线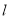 过
过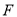 且依次交抛物线及圆
且依次交抛物线及圆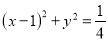 于点
于点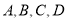 四点,则
四点,则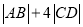 的最小值为( )
的最小值为( )
A.
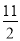 B.
B. 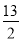 C.
C. 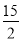 D.
D. 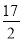
相关试题

