【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过
过![]() 且依次交抛物线及圆
且依次交抛物线及圆![]() 于点
于点![]() 四点,则
四点,则![]() 的最小值为( )
的最小值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】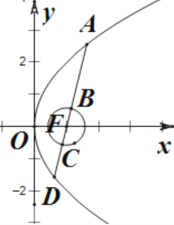
如图所示,抛物线![]() 的焦点
的焦点![]() ,圆
,圆![]() 的圆心坐标是
的圆心坐标是![]() ,半径
,半径![]() ,设
,设![]() ,由抛物线的定义可知
,由抛物线的定义可知![]() ,
, ![]()
![]() ,显然直线
,显然直线![]() 不可能平行于
不可能平行于![]() 轴,设直线
轴,设直线![]() 的方程为
的方程为![]() 代入到抛物线的方程中,得
代入到抛物线的方程中,得![]() ,
, ![]() ,显然
,显然![]() ,
, ![]() ,等号成立当且仅当
,等号成立当且仅当![]() 和
和![]() 同时成立,即等号成立当且仅当
同时成立,即等号成立当且仅当![]() ,
, ![]() 的最小值是
的最小值是![]() ,故选B.
,故选B.
【 方法点睛】本题主要考查抛物线的定义和几何性质,以及基本不等式求最值,属于难题. 与焦点、准线有关的问题一般情况下都与拋物线的定义有关,解决这类问题一定要注意点到点的距离与点到直线的距离的转化:(1)将抛线上的点到准线距转化为该点到焦点的距离;(2)将抛物线上的点到焦点的距离转化为到准线的距离,本题就是将![]() 转化为到准线的距离后,再利用韦达定理与基本不等式使问题得到解决的.
转化为到准线的距离后,再利用韦达定理与基本不等式使问题得到解决的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,已知曲线
中,已知曲线 的参数方程为
的参数方程为 (
( 为参数),以直角坐标系原点
为参数),以直角坐标系原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的普通方程与直线
的普通方程与直线 的直角坐标方程;
的直角坐标方程;(Ⅱ)设点
 为曲线
为曲线 上的动点,求点
上的动点,求点 到直线
到直线 距离的最大值及其对应的点
距离的最大值及其对应的点 的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x),对任意a,b∈R,都有f(a+b)=f(a)+f(b)﹣1,当x>0时,f(x)>1;且f(2)=3,
(1)求f(0)及f(1)的值;
(2)判断函数f(x)在R上的单调性,并给予证明;
(3)若f(﹣kx2)+f(kx﹣2)<2对任意的x∈R恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
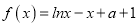 .
.(Ⅰ)若存在
 使得
使得 成立,求实数
成立,求实数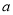 的取值范围;
的取值范围;(Ⅱ)求证:当
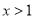 时,在(1)的条件下,
时,在(1)的条件下, 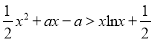 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线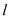 的参数方程为
的参数方程为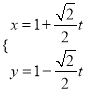 (
(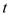 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以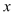 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆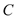 的极坐标方程为
的极坐标方程为 ,圆
,圆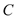 与直线
与直线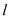 交于
交于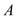 ,
,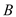 两点,
两点,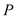 点的直角坐标为
点的直角坐标为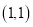 .
.(1)将直线
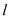 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆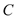 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(2)求
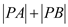 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数f(x)=x2+bx+c满足f(2)=f(﹣2),且函数的f(x)的一个根为1.
(1)求函数f(x)的解析式;
(2)对任意的x∈[ ,+∞),方程4mf(x)+f(x﹣1)=4﹣4m有解,求实数m的取值范围.
,+∞),方程4mf(x)+f(x﹣1)=4﹣4m有解,求实数m的取值范围.
相关试题

