【题目】已知![]() 为坐标原点,
为坐标原点, ![]() 是椭圆
是椭圆![]() 上的点,设动点
上的点,设动点![]() 满足
满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两个不同点,求
两个不同点,求![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设点![]() ,,则由
,,则由![]() ,得
,得![]() ,利用“逆代法”可得动点
,利用“逆代法”可得动点![]() 的轨迹
的轨迹![]() 的方程;(2)直线
的方程;(2)直线![]() 与曲线
与曲线![]() ,联立可得
,联立可得![]() ,,根据韦达定理,弦长公式、点到直线距离公式将
,,根据韦达定理,弦长公式、点到直线距离公式将![]() 面积用
面积用![]() 表示,利用基本不等式 即可得结.
表示,利用基本不等式 即可得结.
试题解析:(1)设点![]() ,
,![]() ,则由
,则由![]() ,得
,得![]() ,即
,即![]() ,
,![]() ,因为点
,因为点![]() 在椭圆
在椭圆![]() ,所以
,所以![]() ,故
,故![]() ,即动点
,即动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由曲线![]() 与直线
与直线![]() 联立得
联立得![]() ,消
,消![]() 得
得![]() ,因为直线
,因为直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,所以
两点,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,因为点
,因为点![]() 到直线
到直线![]() :
: ![]() 的距离
的距离![]() ,
,![]()
![]()
![]()
![]() ,所以
,所以![]()
![]() ,
,![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,所以
时取等号,所以![]() 面积的最大值为
面积的最大值为![]() .
.
【方法点晴】本题主要考查逆代法求曲线方程及圆锥曲线求最值,属于难题.解决圆锥曲线中的最值问题一般有两种方法:一是几何意义,特别是用圆锥曲线的定义和平面几何的有关结论来解决,非常巧妙;二是将圆锥曲线中最值问题转化为函数问题,然后根据函数的特征选用参数法、配方法、判别式法、三角函数有界法、函数单调性法以及均值不等式法,本题(2)就是用的这种思路,利用均值不等式法求三角形最大值的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|(x﹣a)[x﹣(a+3)]≤0}(a∈R),B={x|x2﹣4x﹣5>0}.
(1)若A∩B=,求实数a的取值范围;
(2)若A∪B=B,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
轿车A
轿车B
轿车C
舒适型
100
150
z
标准型
300
450
600
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 过点
过点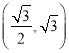 ,离心率为
,离心率为 .
.(1)求椭圆的标准方程;
(2)过椭圆的上顶点作直线
 交抛物线
交抛物线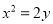 于
于 两点,
两点,  为原点.
为原点.①求证:
 ;
;②设
 、
、 分别与椭圆相交于
分别与椭圆相交于 、
、 两点,过原点
两点,过原点 作直线
作直线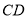 的垂线
的垂线 ,垂足为
,垂足为 ,证明:
,证明:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】中心在原点,焦点在x轴上的一椭圆与一双曲线有共同的焦点F1,F2,且|F1F2|=
 ,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7.
,椭圆的长半轴与双曲线实半轴之差为4,离心率之比为3∶7. (1)求这两曲线的方程;
(2)若P为这两曲线的一个交点,求cos∠F1PF2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,已知曲线
中,已知曲线 的参数方程为
的参数方程为 (
( 为参数),以直角坐标系原点
为参数),以直角坐标系原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的普通方程与直线
的普通方程与直线 的直角坐标方程;
的直角坐标方程;(Ⅱ)设点
 为曲线
为曲线 上的动点,求点
上的动点,求点 到直线
到直线 距离的最大值及其对应的点
距离的最大值及其对应的点 的直角坐标.
的直角坐标.
相关试题

