【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意程度进行调查,并随机抽取了其中30名员工(16名女工,14名男工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平局得分为 “满意”,否则为 “不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 16 | ||
男员工 | 14 | ||
合计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
P(K2 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]()
参考答案:
【答案】(1)240;(2)见解析;(3)见解析
【解析】分析:第一问首先从表中查找得分大于45分的人数,求得比值即为概率,应用对应的关系式求得相应的人数;第二问按照条件,将男女员工对应的分数分析比较,进行分类,从而将相应的数据填入表中,得到列联表;第三问利用公式求得观测值,判断出结果即可.
详解:(1)从表中可知,30名员工有8名得分大于45分,所以任选一名员工,他(她)的得分大于45分的概率是![]() ,所以估计此次调查中,该单位约有
,所以估计此次调查中,该单位约有![]() 名员工的得分大于45分;
名员工的得分大于45分;
(2)依题意,完成![]() 列联表如下:
列联表如下:
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 12 | 4 | 16 |
男员工 | 3 | 11 | 14 |
合计 | 15 | 15 | 30 |
(3)假设![]() :性别与工作是否满意无关,根据表中数据,求得
:性别与工作是否满意无关,根据表中数据,求得![]() 的观测值:
的观测值:
![]()
查表得![]()
![]() 能在犯错误的概率不超过1%的前提下,认为性别与工作是否满意有关.
能在犯错误的概率不超过1%的前提下,认为性别与工作是否满意有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形
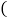 如图
如图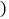 ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为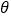 ,则
,则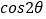 等于
等于

A.
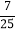 B.
B.  C.
C. 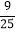 D.
D. 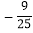
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,的部分图象如图所示.
,的部分图象如图所示.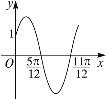
(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)求函数
 的单调递增区间.
的单调递增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数y=sin3x+cos3x的图象,可以将函数y=
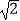 cos3x的图象( )
cos3x的图象( )
A.向右平移 个单位
个单位
B.向左平移 个单位
个单位
C.向右平移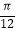 个单位
个单位
D.向左平移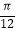 个单位
个单位 -
科目: 来源: 题型:
查看答案和解析>>【题目】禽流感一直在威胁我们的生活,某疾病控制中心为了研究禽流感病毒繁殖个数
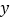 (个)随时间
(个)随时间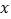 (天)变化的规律,收集数据如下:
(天)变化的规律,收集数据如下:天数
1
2
3
4
5
6
繁殖个数
6
12
25
49
95
190
作出散点图可看出样本点分布在一条指数型函数
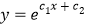 的周围.
的周围.保留小数点后两位数的参考数据:
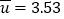 ,
,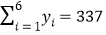 ,
, ,
,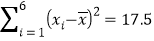 ,
,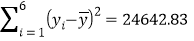 ,
,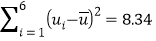 ,
,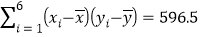 ,
,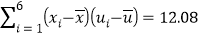 ,其中
,其中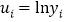
(1)求出
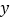 关于
关于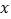 的回归方程(保留小数点后两位数字);
的回归方程(保留小数点后两位数字);(2)已知
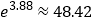 ,估算第四天的残差.
,估算第四天的残差.参考公式:
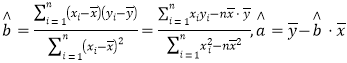
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点
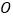 为极点,
为极点,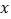 轴的正半轴为极轴,且两个坐标系取相等的长度单位建立坐标系.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位建立坐标系.已知直线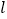 的极坐标方程为
的极坐标方程为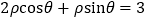 ,曲线
,曲线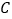 的参数方程为
的参数方程为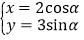 (
(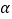 为参数).
为参数). (1)求曲线
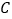 的普通方程和直线
的普通方程和直线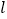 的直角坐标方程;
的直角坐标方程;(2)直线
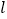 上有一点
上有一点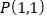 ,设直线
,设直线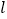 与曲线
与曲线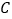 相交于
相交于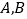 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】记max{x,y}=
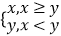 ,min{x,y}=
,min{x,y}= 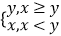 ,设
,设 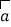 ,
,  为平面向量,则( )
为平面向量,则( )
A.min{| +
+ 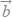 |,|
|,|  ﹣
﹣ 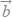 |}≤min{|
|}≤min{|  |,|
|,| 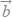 |}
|}
B.min{| +
+ 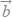 |,|
|,|  ﹣
﹣ 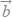 |}≥min{|
|}≥min{|  |,|
|,| 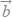 |}
|}
C.max{| +
+ 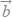 |2 , |
|2 , |  ﹣
﹣ 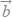 |2}≤|
|2}≤|  |2+|
|2+| 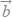 |2
|2
D.max{| +
+ 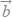 |2 , |
|2 , |  ﹣
﹣ 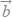 |2}≥|
|2}≥| |2+| 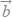 |2
|2
相关试题

