【题目】如图,四棱锥![]() 的底面是边长为1的正方形,侧棱
的底面是边长为1的正方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是侧棱
是侧棱![]() 上的动点.
上的动点.
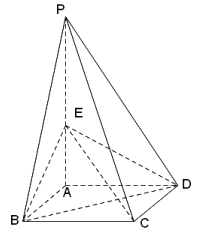
(Ⅰ)求四棱锥![]() 的体积;
的体积;
(Ⅱ)如果![]() 是
是![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅲ)是否不论点![]() 在侧棱
在侧棱![]() 的任何位置,都有
的任何位置,都有![]() ?证明你的结论.
?证明你的结论.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)不论点
;(Ⅱ)见解析;(Ⅲ)不论点![]() 在何位置,都有
在何位置,都有![]() .
.
【解析】试题分析:(Ⅰ) ![]() 平面
平面![]() 知棱锥得高即为
知棱锥得高即为![]() ,所以根据体积公式得:
,所以根据体积公式得: ![]() .(Ⅱ)连结
.(Ⅱ)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
根据中位线知![]() ,由线面平行的判定定理知
,由线面平行的判定定理知![]() 平面
平面![]() .(Ⅲ)不论点
.(Ⅲ)不论点![]() 在何位置,都有
在何位置,都有![]() .由题意易知
.由题意易知![]() 平面
平面![]() .所以不论点
.所以不论点![]() 在何位置,都有
在何位置,都有![]() 平面
平面![]() ,故都有
,故都有![]() .
.
试题解析:(Ⅰ)∵![]() 平面
平面![]() ,
,
∴![]() ,
,
即四棱锥![]() 的体积为
的体积为![]() .
.
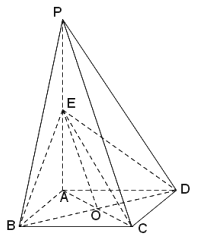
(Ⅱ)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
∵四边形![]() 是正方形,∴
是正方形,∴![]() 是
是![]() 的中点,
的中点,
又∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)不论点![]() 在何位置,都有
在何位置,都有![]() .
.
证明如下:∵四边形![]() 是正方形,∴
是正方形,∴![]() ,
,
∵![]() 底面
底面![]() ,且
,且![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∵不论点![]() 在何位置,都有
在何位置,都有![]() 平面
平面![]() ,
,
∴不论点![]() 在何位置,都有
在何位置,都有![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
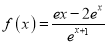 ,
,  .
.(Ⅰ)求函数
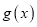 在区间
在区间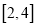 上的最小值;
上的最小值;(Ⅱ)证明:对任意
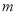 ,
, 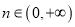 ,都有
,都有 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】运货卡车以每小时
 千米的速度匀速行驶
千米的速度匀速行驶 千米(
千米( ).假设汽油的价格是每升
).假设汽油的价格是每升 元,而汽车每小时耗油
元,而汽车每小时耗油 升,司机的工资是每小时
升,司机的工资是每小时 元.
元.(1)求这次行车总费用
 关于
关于 的表达式;
的表达式;(2)当
 为何值时,这次行车的总费用最低?并求出最低费用的值.
为何值时,这次行车的总费用最低?并求出最低费用的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】股票市场的前身是起源于1602年荷兰人在阿姆斯特河大桥上进行荷属东印度公司股票的买卖,而正规的股票市场最早出现在美国.2017年2月26号,中国证监会主席刘士余谈了对股市的几点建议,给广大股民树立了信心.最近,张师傅和李师傅要将家中闲置资金进行投资理财.现有两种投资方案,且一年后投资盈亏的情况如下:
(1)投资股市:
投资结果
获利
不赔不赚
亏损
概率



(2)购买基金:
投资结果
获利
不赔不赚
亏损
概率



(Ⅰ)当
 时,求
时,求 的值;
的值;(Ⅱ)已知“购买基金”亏损的概率比“投资股市”亏损的概率小,求
 的取值范围;
的取值范围;(Ⅲ)已知张师傅和李师傅两人都选择了“购买基金”来进行投资,假设三种投资结果出现的可能性相同,求一年后他们两人中至少有一人获利的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
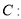
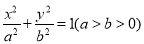 ,
, 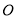 是坐标原点,
是坐标原点,  分别为其左右焦点,
分别为其左右焦点, 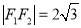 ,
, 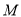 是椭圆上一点,
是椭圆上一点, 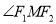 的最大值为
的最大值为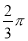
(Ⅰ)求椭圆
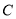 的方程;
的方程;(Ⅱ)若直线
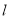 与椭圆
与椭圆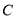 交于
交于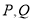 两点,且
两点,且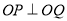
(i)求证:
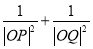 为定值;
为定值;(ii)求
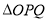 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<
 )的部分图象如图所示,则f(x)的解析式为( )
)的部分图象如图所示,则f(x)的解析式为( ) 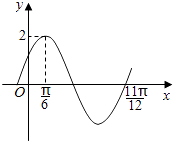
A.f(x)=2sin(x+ )
)
B.f(x)=2sin(2x+ )
)
C.f(x)=2sin(2x﹣ )
)
D.f(x)=2sin(4x﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=
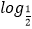 (1﹣x).
(1﹣x).
(1)求f(0),f(1);
(2)求函数f(x)的解析式.
相关试题

