【题目】已知函数f(x)=3ax2+2bx+c,a+b+c=0,f(0)>0,f(1)>0,证明a>0,并利用二分法证明方程f(x)=0在区间[0,1]内有两个实根.
参考答案:
【答案】见解析
【解析】试题分析:根据函数解析式代入f(0)>0、f(1)>0,得c>0且3a+2b+c>0,结合a+b+c=0化简即可得到a>0;利用a+b+c=0化简得f(![]() )=-
)=- ![]() ,结合a>0,可得f(
,结合a>0,可得f(![]() )<0,由f(
)<0,由f(![]() )与f(0),f(1)都异号,利用零点存在性定理得f(x)=0在区间
)与f(0),f(1)都异号,利用零点存在性定理得f(x)=0在区间![]() 和
和![]() 上各有一个零点,由此可得f(x)=0在区间[0,1]内有两个实根.
上各有一个零点,由此可得f(x)=0在区间[0,1]内有两个实根.
试题解析:
∵f(1)>0,∴3a+2b+c>0,
即3(a+b+c)-b-2c>0.
∵a+b+c=0,∴-b-2c>0,
则-b-c>c,即a>c.
∵f(0)>0,∴c>0,则a>0.
在区间[0,1]内选取二等分点![]() ,
,
则f![]() =
=![]() a+b+c=
a+b+c=![]() a+(-a)=-
a+(-a)=-![]() a<0.
a<0.
∵f(0)>0,f(1)>0,
∴函数f(x)在区间![]() 和
和![]() 上各有一个零点.
上各有一个零点.
又f(x)最多有两个零点,从而f(x)=0在[0,1]内有两个实根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
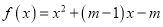 ,
, 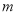 为实数.
为实数.(1)若关于
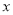 的不等式
的不等式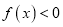 的解集为
的解集为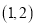 ,求实数
,求实数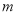 的值;
的值; (2)设
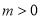 ,当
,当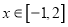 时,求函数
时,求函数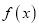 的最小值(用
的最小值(用 表示);
表示);(3)若关于
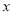 不等式
不等式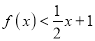 的解集中恰好有两个整数解,求
的解集中恰好有两个整数解,求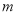 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(-x2+x-1)ex,其中e是自然对数的底数.
(1)求曲线f(x)在点(1,f(1))处的切线;
(2)若方程f(x)=
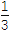 x3+
x3+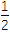 x2+m有3个不同的根,求实数m的取值范围.
x2+m有3个不同的根,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017唐山模拟】如图,ABCDA1B1C1D1为正方体,连接BD,AC1,B1D1,CD1,B1C,现有以下几个结论:①BD∥平面CB1D1;②AC1⊥平面CB1D1;③AC1与底面ABCD所成角的正切值是
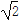 ;④CB1与BD为异面直线,其中所有正确结论的序号为________.
;④CB1与BD为异面直线,其中所有正确结论的序号为________.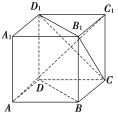
-
科目: 来源: 题型:
查看答案和解析>>【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用K、A1、A2三类不同的元件连接成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )
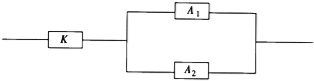
A. 0.960 B. 0.864 C. 0.720 D. 0.576
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
相关试题

