【题目】已知函数f(x)=lg(ax-bx),(a>1>b>0).
(1)求f(x)的定义域;
(2)若f(x)在(1,+∞)上递增且恒取正值,求a,b满足的关系式.
参考答案:
【答案】(1) ![]() ; (2)
; (2) ![]()
【解析】试题分析:(1)要求ax﹣bx>0,变量集中得(![]() )x>1,利用指数函数性质求解;
)x>1,利用指数函数性质求解;
(2)由增函数可得f(x)>f(1),只需f(1)=lg(a﹣b)≥0即可得到a-b≥1.
试题解析:
(1)由ax-bx>0,得![]() >1.
>1.
因为a>1>b>0,所以![]() >1.所以x>0.
>1.所以x>0.
所以f(x)的定义域为(0,+∞).
(2)因为f(x)在(1,+∞)上递增且恒为正值,
所以f(x)>f(1),只要f(1)>0.
则lg(a-b)≥0,所以a-b≥1.
因此a,b满足的关系为a≥b+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=3ax2+2bx+c,a+b+c=0,f(0)>0,f(1)>0,证明a>0,并利用二分法证明方程f(x)=0在区间[0,1]内有两个实根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设人的某一特征(如眼睛的大小)是由他的一对基因所决定,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,纯显性与混合性的人都显露显性基因决定的某一特征,孩子从父母身上各得到一个基因,假定父母都是混合性,问:
(1)1个孩子显露显性特征的概率是多少?
(2)“该父母生的2个孩子中至少有1个显露显性特征”,这种说法正确吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用K、A1、A2三类不同的元件连接成一个系统.当K正常工作且A1、A2至少有一个正常工作时,系统正常工作,已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为( )
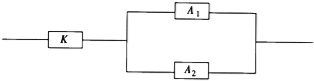
A. 0.960 B. 0.864 C. 0.720 D. 0.576
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,空气质量成为人们越来越关注的话题,空气质量指数(
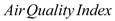 ,简称
,简称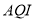 )是定量描述空气质量状况的指数,空气质量按照
)是定量描述空气质量状况的指数,空气质量按照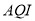 大小分为六级,
大小分为六级, 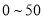 为优;
为优;  为良;
为良; 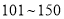 为轻度污染;
为轻度污染; 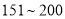 为中度污染;
为中度污染; 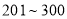 为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的
为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的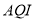 的茎叶图如下:
的茎叶图如下:
(1)利用该样本估计该地本月空气质量优良(
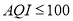 )的天数;(按这个月总共30天计算)
)的天数;(按这个月总共30天计算)(2)现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究,求抽取的2天中至少有一天空气质量是优的概率;
(3)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为
 ,求
,求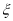 的概率分布列和数学期望.
的概率分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司从1999年的年产值100万元,增加到10年后2009年的500万元,如果每年产值增长率相同,则每年的平均增长率是多少?(ln(1+x)≈x,lg2=0.3,ln10=2.30)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①分类变量
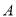 与
与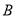 的随机变量
的随机变量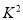 越大,说明“
越大,说明“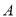 与
与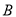 有关系”的可信度越大.
有关系”的可信度越大.②以模型
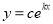 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设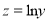 ,将其变换后得到线性方程
,将其变换后得到线性方程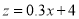 ,则
,则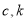 的值分别是
的值分别是 和0.3.
和0.3.③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
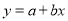 中,
中, 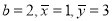 ,则
,则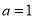 .
.④如果两个变量
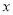 与
与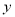 之间不存在着线性关系,那么根据它们的一组数据
之间不存在着线性关系,那么根据它们的一组数据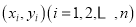 不能写出一个线性方程
不能写出一个线性方程正确的个数是( )
A. 1 B. 2 C. 3 D. 4
相关试题

