【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
参考答案:
【答案】解:设投资人对甲、乙两个项目各投资x和y万元,则 ![]() ,设z=x+0.5y=0.25(x+y)+0.25(3x+y)≤0.25×10+0.25×18=7,
,设z=x+0.5y=0.25(x+y)+0.25(3x+y)≤0.25×10+0.25×18=7,
当 ![]() 即
即 ![]() 时,z取最大值7万元
时,z取最大值7万元
答:投资人对甲、乙两个项目分别投资4万元和6万元时,才能使可能的盈利最大
【解析】设投资人对甲、乙两个项目各投资x和y万元,列出x和y的不等关系 ![]() 及目标函数z=x+0.5y.利用线性规划或不等式的性质求最值即可.
及目标函数z=x+0.5y.利用线性规划或不等式的性质求最值即可.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 x3﹣x2+x.
x3﹣x2+x.
(1)求函数f(x)在[﹣1,2]上的最大值和最小值;
(2)若函数g(x)=f(x)﹣4x,x∈[﹣3,2],求g(x)的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A、B、C所对的边分别为a,b,c且a=5,sinA=
 .
.
(I)若S△ABC= ,求周长l的最小值;
,求周长l的最小值;
(Ⅱ)若cosB= ,求边c的值.
,求边c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
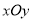 中,已知曲线
中,已知曲线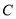 的参数方程为
的参数方程为 (
(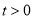 ,
, 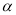 为参数).以坐标原点
为参数).以坐标原点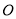 为极点,
为极点, 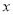 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线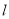 的极坐标方程为
的极坐标方程为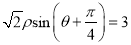 .
.(1)当
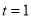 时,求曲线
时,求曲线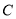 上的点到直线
上的点到直线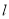 的距离的最大值;
的距离的最大值;(2)若曲线
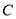 上的所有点都在直线
上的所有点都在直线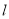 的下方,求实数
的下方,求实数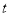 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足an+1+an=4n﹣3(n∈N*)
(Ⅰ)若{an}是等差数列,求其通项公式;
(Ⅱ)若{an}满足a1=2,Sn为{an}的前n项和,求S2n+1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
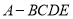 ,其中
,其中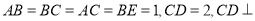 面
面 为
为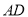 的中点.
的中点.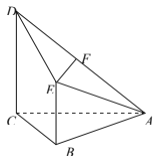
(1)求证:
 面
面 ;
;(2)求证:面
 面
面 ;
;(3)求四棱锥
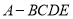 的体积.
的体积.
相关试题

