【题目】数列{an}满足an+1+an=4n﹣3(n∈N*)
(Ⅰ)若{an}是等差数列,求其通项公式;
(Ⅱ)若{an}满足a1=2,Sn为{an}的前n项和,求S2n+1 .
参考答案:
【答案】解:( I)由题意得an+1+an=4n﹣3…①an+2+an+1=4n+1…②.
②﹣①得an+2﹣an=4,
∵{an}是等差数列,设公差为d,∴d=2,
∵a1+a2=1∴a1+a1+d=1,∴ ![]() .
.
∴ ![]() .
.
(Ⅱ)∵a1=2,a1+a2=1,
∴a2=﹣1.
又∵an+2﹣an=4,
∴数列的奇数项与偶数项分别成等差数列,公差均为4,
S2n+1=(a1+a3+…+a2n+1)+(a2+a4+…+a2n)
= ![]()
=4n2+n+2
【解析】(Ⅰ)由题意得an+1+an=4n﹣3,an+2+an+1=4n+1.所以an+2﹣an=4,由{an}是等差数列,公差d=2,能求出 ![]() .(Ⅱ)由a1=2,a1+a2=1,知a2=﹣1.因为an+2﹣an=4,所以数列的奇数项与偶数项分别成等差数列,公差均为4,故a2n﹣1=4n﹣2,a2n=4n﹣5.由此能求出S2n+1 .
.(Ⅱ)由a1=2,a1+a2=1,知a2=﹣1.因为an+2﹣an=4,所以数列的奇数项与偶数项分别成等差数列,公差均为4,故a2n﹣1=4n﹣2,a2n=4n﹣5.由此能求出S2n+1 .
【考点精析】掌握等差数列的通项公式(及其变式)和等差数列的前n项和公式是解答本题的根本,需要知道通项公式:![]() 或
或![]() ;前n项和公式:
;前n项和公式:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A、B、C所对的边分别为a,b,c且a=5,sinA=
 .
.
(I)若S△ABC= ,求周长l的最小值;
,求周长l的最小值;
(Ⅱ)若cosB= ,求边c的值.
,求边c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
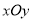 中,已知曲线
中,已知曲线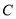 的参数方程为
的参数方程为 (
(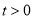 ,
, 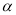 为参数).以坐标原点
为参数).以坐标原点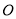 为极点,
为极点, 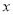 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线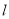 的极坐标方程为
的极坐标方程为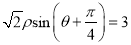 .
.(1)当
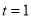 时,求曲线
时,求曲线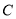 上的点到直线
上的点到直线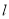 的距离的最大值;
的距离的最大值;(2)若曲线
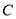 上的所有点都在直线
上的所有点都在直线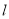 的下方,求实数
的下方,求实数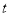 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
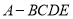 ,其中
,其中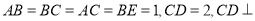 面
面 为
为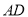 的中点.
的中点.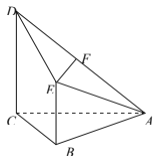
(1)求证:
 面
面 ;
;(2)求证:面
 面
面 ;
;(3)求四棱锥
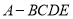 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】对定义域分别为D1 , D2的函数y=f(x),y=g(x),规定:函数h(x)=
 ,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是
,f(x)=x﹣2(x≥1),g(x)=﹣2x+3(x≤2),则h(x)的单调减区间是 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB,位于该市的某大学M与市中心O的距离OM=3
 km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ=
km,且∠AOM=β,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,且经过大学M,其中tanα=2,cosβ= 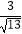 ,AO=15km.
,AO=15km. 
(1)求大学M在站A的距离AM;
(2)求铁路AB段的长AB.
相关试题

