【题目】如图,四棱锥![]() 的底面
的底面![]() 是平行四边形,侧面
是平行四边形,侧面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() ,
, ![]() .
.
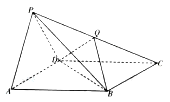
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 是棱
是棱![]() 上的点,当
上的点,当![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)要证平面![]() 平面
平面![]() ,只需证
,只需证![]() 平面
平面![]() 即可.
即可.
(Ⅱ)分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系如图,求平面
轴建立空间直角坐标系如图,求平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的一个法向量求解即可.
的一个法向量求解即可.
试题解析:
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
,
因为![]() 是边长为2的正三角形,所以
是边长为2的正三角形,所以![]() ,
, ![]() ,①
,①
又![]() ,所以
,所以![]() ,且
,且![]() ,
,
于是![]() ,从而
,从而![]() ,②
,②
由①②得![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)连结![]() ,设
,设![]() ,则
,则![]() 为
为![]() 的中点,连结
的中点,连结![]() ,当
,当![]() 平面
平面![]() 时,
时, ![]() ,所以
,所以![]() 是
是![]() 的中点.
的中点.
由(Ⅰ)知, ![]() 、
、![]() 、
、![]() 两两垂直,分别以
两两垂直,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系如图,则
轴建立空间直角坐标系如图,则![]() 、
、![]() 、
、![]() 、
、![]() ,
,
由![]() 、
、![]() 坐标得
坐标得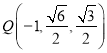 ,从而
,从而![]() ,
, 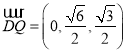 ,
,
设![]() 是平面
是平面![]() 的一个法向量,则由
的一个法向量,则由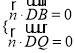 得
得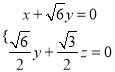 ,
,
取![]() ,得
,得![]() ,易知平面
,易知平面![]() 的一个法向量是
的一个法向量是![]() ,
,
所以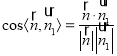
![]() ,
,
由图可知,二面角![]() 的平面角为钝角,故所求余弦值为
的平面角为钝角,故所求余弦值为![]() .
.
-
科目: 来源: 题型:
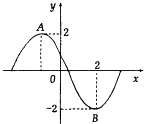
查看答案和解析>>【题目】函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( )
A.y=2sin( x+
x+  )
)
B.y=2sin( x+
x+  )
)
C.y=2sin( x+
x+  )
)
D.y=2sin( x+
x+  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨,现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为
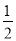 ,后2天均为
,后2天均为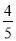 ,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.(1)求至少有1天需要人工降雨的概率;
(2)求不需要人工降雨的天数
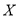 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个结论:
①若α、β为第一象限角,且α>β,则sinα>sinβ
②函数y=|sinx|与y=|tanx|的最小正周期相同
③函数f(x)=sin(x+ )在[﹣
)在[﹣  ,
,  ]上是增函数;
]上是增函数;
④若函数f(x)=asinx﹣bcosx的图象的一条对称轴为直线x= ,则a+b=0.
,则a+b=0.
其中正确结论的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知2sinx=sin( ﹣x),求
﹣x),求  的值;
的值;
(2)求函数f(x)=ln(sinx﹣ )+
)+ 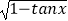 的定义域.
的定义域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
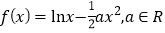 .
.(1)求函数
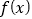 的单调区间;
的单调区间;(2)若关于
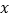 的不等式
的不等式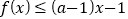 恒成立,求整数
恒成立,求整数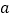 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的公差d>0,设{an}的前n项和为Sn , a1=1,S2S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
相关试题

