【题目】已知等差数列{an}的公差d>0,设{an}的前n项和为Sn , a1=1,S2S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
参考答案:
【答案】
(1)解:由a1=1,S2S3=36得,
(a1+a2)(a1+a2+a3)=36,
即(2+d)(3+3d)=36,化为d2+3d﹣10=0,
解得d=2或﹣5,
又公差d>0,则d=2,
所以Sn=n ![]() =n2(n∈N*).
=n2(n∈N*).
(2)解:由(1)得,an=1+2(n﹣1)=2n﹣1,
由am+am+1+am+2+…+am+k=65得, ![]() ,
,
即(k+1)(2m+k﹣1)=65,
又m,k∈N*,则(k+1)(2m+k﹣1)=5×13,或(k+1)(2m+k﹣1)=1×65,
下面分类求解:
当k+1=5时,2m+k﹣1=13,解得k=4,m=5;
当k+1=13时,2m+k﹣1=5,解得k=12,m=﹣3,故舍去;
当k+1=1时,2m+k﹣1=65,解得k=0,故舍去;
当k+1=65时,2m+k﹣1=1,解得k=64,m=﹣31,故舍去;
综上得,k=4,m=5.
【解析】(1)根据等差数列通项公式和前n项和公式,把条件转化为关于公差d的二次方程求解,注意d的范围对方程的根进行取舍;(2)由(1)求出等差数列{an}的通项公式,利用等差数列的前n项和公式,对am+am+1+am+2+…+am+k=65化简,列出关于m、k的方程,再由m,k∈N*进行分类讨论,求出符合条件的m、k的值.
【考点精析】关于本题考查的等差数列的前n项和公式和数列的前n项和,需要了解前n项和公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系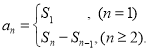 才能得出正确答案.
才能得出正确答案.
-
科目: 来源: 题型:
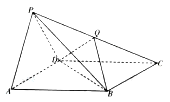
查看答案和解析>>【题目】如图,四棱锥
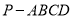 的底面
的底面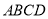 是平行四边形,侧面
是平行四边形,侧面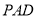 是边长为2的正三角形,
是边长为2的正三角形,  ,
, 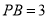 .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)设
 是棱
是棱 上的点,当
上的点,当 平面
平面 时,求二面角
时,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)已知2sinx=sin( ﹣x),求
﹣x),求  的值;
的值;
(2)求函数f(x)=ln(sinx﹣ )+
)+ 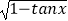 的定义域.
的定义域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
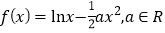 .
.(1)求函数
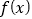 的单调区间;
的单调区间;(2)若关于
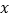 的不等式
的不等式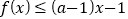 恒成立,求整数
恒成立,求整数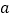 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次抽样调查中测得样本的6组数据,得到一个变量
 关于
关于 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表:
2
3
4
5
6
7







(1)请用相关系数
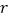 加以说明
加以说明 与
与 之间存在线性相关关系(当
之间存在线性相关关系(当 时,说明
时,说明 与
与 之间具有线性相关关系);
之间具有线性相关关系);(2)根据(1)的判断结果,建立
 关于
关于 的回归方程并预测当
的回归方程并预测当 时,对应的
时,对应的 值为多少(
值为多少( 精确到
精确到 ).
).附参考公式:回归方程
 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: ,
, ,相关系数
,相关系数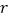 公式为:
公式为: .
.参考数据:
 ,
, ,
, ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
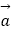 =(cosωx,sinωx),
=(cosωx,sinωx), 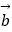 =(cosωx,
=(cosωx, 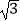 cosωx),其中ω>0,设函数f(x)=
cosωx),其中ω>0,设函数f(x)= 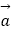
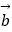 .
.
(1)若函数f(x)的最小正周期是π,求函数f(x)的单调递增区间;
(2)若函数f(x)的图象的一个对称中心的横坐标为 ,求ω的最小值.
,求ω的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: 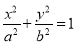 (
( )的离心率为
)的离心率为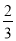 ,
,  、
、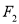 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线 ,使
,使 、
、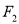 关于
关于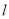 的对称点恰好是圆
的对称点恰好是圆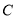 :
: 
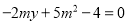 (
( ,
,  )的一条直径的两个端点.
)的一条直径的两个端点.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设直线
 与抛物线
与抛物线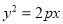 (
( )相交于
)相交于 、
、 两点,射线
两点,射线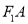 、
、 与椭圆
与椭圆 分别相交于点
分别相交于点 、
、 .试探究:是否存在数集
.试探究:是否存在数集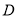 ,当且仅当
,当且仅当 时,总存在
时,总存在 ,使点
,使点 在以线段
在以线段 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集 ;若不存在,请说明理由.
;若不存在,请说明理由.
相关试题

