【题目】如果二面角α﹣L﹣β的大小是60°,线段AB在α内,AB与L所成的角为60°,则AB与平面β所成角的正切值是 .
参考答案:
【答案】![]()
【解析】解:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线,垂足为D. 连结AD,根据三垂线定理可得AD⊥L,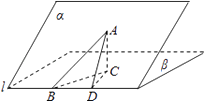
因此,∠ADC为二面角α﹣L﹣β的平面角,∠ADC=60°
又∵AB与L所成角为60°,
∴∠ABD=60°,
连结BC,可得BC为AB在平面β内的射影,
∴∠ABC为AB与平面β所成的角.
设AD=2x,则Rt△ACD中,AC=ADsin60°= ![]() x,
x,
Rt△ABD中,AB= ![]() =
= ![]() x
x
∴Rt△ABC中,sin∠ABC= ![]() =34,
=34,
∴tan∠ABC= ![]()
所以答案是: ![]() .
.
【考点精析】掌握空间角的异面直线所成的角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则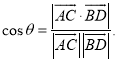 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣
 )的定义域为( )
)的定义域为( )
A.[ ,
,  ]
]
B.[1, ]
]
C.[﹣1, ]
]
D.[﹣1, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)+g(x)=2x , 则有( )
A.f(3)<g(0)<f(4)
B.g(0)<f(4)<f(3)
C.g(0)<f(3)<f(4)
D.f(3)<f(4)<g(0) -
科目: 来源: 题型:
查看答案和解析>>【题目】非空集合A中的元素个数用(A)表示,定义(A﹣B)=
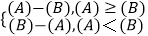 ,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
A.{a|a≥4}
B.{a|a>4或a=0}
C.{a|0≤a≤4}
D.{a|a≥4或a=0} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的函数,满足f(x)=﹣f(﹣x),且当x<0时,f(x)=x
 ,则f(9)= .
,则f(9)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面是矩形,PA⊥底面ABCD,PA=AD,点E、F分别为棱AB、PD的中点. (Ⅰ)求证:AF∥平面PCE;
(Ⅱ)AD与平面PCD所成的角的大小.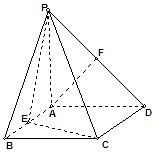
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数f(x)定义域内的任意x1 , x2(x1≠x2),有以下结论:
①f(0)=1;
②f(1)=0
③f(x1+x2)=f(x1)f(x2)
④f(x1x2)=f(x1)+f(x2)
⑤f(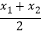 )<
)< 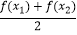
⑥f(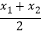 )>
)> 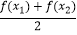
当f(x)=2x时,则上述结论中成立的是(填入你认为正确的所有结论的序号)
相关试题

