【题目】对于函数f(x)定义域内的任意x1 , x2(x1≠x2),有以下结论:
①f(0)=1;
②f(1)=0
③f(x1+x2)=f(x1)f(x2)
④f(x1x2)=f(x1)+f(x2)
⑤f( ![]() )<
)< ![]()
⑥f( ![]() )>
)> ![]()
当f(x)=2x时,则上述结论中成立的是(填入你认为正确的所有结论的序号)
参考答案:
【答案】①③⑤
【解析】解:对于①:f(0)=20=1,故①正确;
对于②:f(1)=2,故②错误;
对于③:根据分数指数幂的运算性质可知,f(x1+x2)=2x1+x2= ![]() =f(x1)f(x2),故③正确;
=f(x1)f(x2),故③正确;
对于④:根据分数指数幂的运算性质可知,f(x1x2)= ![]() =
= ![]() ,
, ![]() .则f(x1x2)≠f(x1)+f(x2),故④错误;
.则f(x1x2)≠f(x1)+f(x2),故④错误;
对于⑤⑥:根据基本不等式和分数指数幂的运算性质可知.由于 ![]() =
= ![]()
![]() ,
, ![]() =
= ![]() ,
,
所以 ![]() ,故⑤正确,⑥错误.
,故⑤正确,⑥错误.
所以答案是:①③⑤.
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二面角α﹣L﹣β的大小是60°,线段AB在α内,AB与L所成的角为60°,则AB与平面β所成角的正切值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的函数,满足f(x)=﹣f(﹣x),且当x<0时,f(x)=x
 ,则f(9)= .
,则f(9)= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面是矩形,PA⊥底面ABCD,PA=AD,点E、F分别为棱AB、PD的中点. (Ⅰ)求证:AF∥平面PCE;
(Ⅱ)AD与平面PCD所成的角的大小.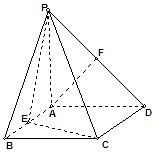
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={y|2<y<3},B={x|(
 )
) 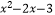 <22(x+1)}.
<22(x+1)}.
(1)求A∩B;
(2)求C={x|x∈B且xA}. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
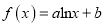 (
(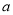 ,
, 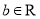 ),曲线
),曲线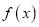 在
在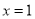 处的切线方程为
处的切线方程为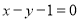 .
.(Ⅰ)求
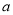 ,
, 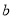 的值;
的值;(Ⅱ)证明:
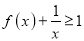 ;
;(Ⅲ)已知满足
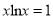 的常数为
的常数为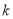 .令函数
.令函数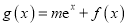 (其中
(其中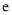 是自然对数的底数,
是自然对数的底数, 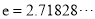 ),若
),若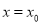 是
是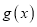 的极值点,且
的极值点,且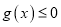 恒成立,求实数
恒成立,求实数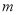 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点
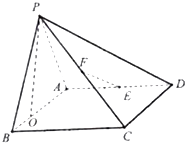
(1)求证:EF⊥平面PBC
(2)若直线PC与平面ABCD所成角为 ,点P在AB上的射影O在靠近点B的一侧,求二面角P﹣EF﹣A的余弦值.
,点P在AB上的射影O在靠近点B的一侧,求二面角P﹣EF﹣A的余弦值.
相关试题

