【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)+g(x)=2x , 则有( )
A.f(3)<g(0)<f(4)
B.g(0)<f(4)<f(3)
C.g(0)<f(3)<f(4)
D.f(3)<f(4)<g(0)
参考答案:
【答案】C
【解析】解:函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)+g(x)=2x ①,
∴f(﹣x)+g(﹣x)=2﹣x , 即﹣f(x)+g(x)=2﹣x ②,
由①②求得f(x)= ![]() ,g(x)=
,g(x)= ![]() ,
,
∴g(0)=1,f(3)= ![]() ,f(4)=8﹣
,f(4)=8﹣ ![]() ,∴g(0)<f(3)<f(4),
,∴g(0)<f(3)<f(4),
故选:C.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方体ABCD﹣A1B1C1D1中,AB=2
 ,AD=2
,AD=2  ,AA1=2,BC和A1C1所成的角=度 AA1和BC1所成的角=度.
,AA1=2,BC和A1C1所成的角=度 AA1和BC1所成的角=度. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的两个函数是同一函数的为( )
(1)f(x)=1,g(x)=x0
(2)f(x)=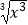 ,g(x)=
,g(x)= 
(3)f(x)=lnxx , g(x)=elnx
(4)f(x)= ,g(x)=
,g(x)=  .
.
A.(1)
B.(2)
C.(3)
D.(4) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为[﹣1,2],则函数g(x)=f(2x﹣
 )的定义域为( )
)的定义域为( )
A.[ ,
,  ]
]
B.[1, ]
]
C.[﹣1, ]
]
D.[﹣1, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】非空集合A中的元素个数用(A)表示,定义(A﹣B)=
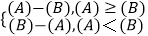 ,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
,若A={﹣1,0},B={x||x2﹣2x﹣3|=a},且(A﹣B)≤1,则a的所有可能值为( )
A.{a|a≥4}
B.{a|a>4或a=0}
C.{a|0≤a≤4}
D.{a|a≥4或a=0} -
科目: 来源: 题型:
查看答案和解析>>【题目】如果二面角α﹣L﹣β的大小是60°,线段AB在α内,AB与L所成的角为60°,则AB与平面β所成角的正切值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的函数,满足f(x)=﹣f(﹣x),且当x<0时,f(x)=x
 ,则f(9)= .
,则f(9)= .
相关试题

