【题目】已知 ![]() ,其中向量
,其中向量 ![]() (x∈R),
(x∈R),
(1)求函数y=f(x)的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别为a、b、c,已知f (A)=2,a= ![]() ,b=
,b= ![]() ,求边长c的值.
,求边长c的值.
参考答案:
【答案】
(1)解:f (x)= ![]() =
= ![]() sin2x+cos2x
sin2x+cos2x
=2sin(2x+ ![]() )
)
由 ![]() ,
,
得 ![]() .
.
∴f(x)的单调增区间为 ![]()
(2)解:f (A)=2sin(2A+ ![]() )=2,
)=2,
∴sin(2A+ ![]() )=1,
)=1,
∵0<A<π,
∴ ![]() ,
,
∴2A+ ![]() =
= ![]() ,
,
∴A= ![]() .
.
由余弦定理得 a2=b2+c2﹣2bccosA,
7=3+c2﹣3c 即 c2﹣3c﹣4=0,
∴c=4或c=﹣1 (不合题意,舍去),
∴c=4
【解析】(1)利用平面向量数量积的运算,两角和的正弦函数公式可求函数解析式为f (x)=2sin(2x+ ![]() ),利用正弦函数的单调性即可得解.(2)由已知可得sin(2A+
),利用正弦函数的单调性即可得解.(2)由已知可得sin(2A+ ![]() )=1,结合范围0<A<π,可求A的值,由余弦定理即可解得c的值.
)=1,结合范围0<A<π,可求A的值,由余弦定理即可解得c的值.
【考点精析】解答此题的关键在于理解余弦定理的定义的相关知识,掌握余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱
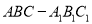 中,
中, 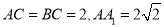 ,∠ACB=90°,M是
,∠ACB=90°,M是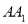 的中点,N是
的中点,N是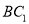 的中点.
的中点.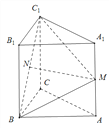
(Ⅰ)求证:MN∥平面
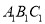 ;
;(Ⅱ)求点
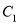 到平面BMC的距离.
到平面BMC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,且a2=﹣14,a5=﹣5.
(1)求数列{an}的通项an;
(2)求{an}前n项和Sn的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.
(1)求f(x)的极值;
(2)当0<x<e时,求证:f(e+x)>f(e﹣x);
(3)设函数f(x)图象与直线y=m的两交点分别为A(x1 , f(x1)、B(x2 , f(x2)),中点横坐标为x0 , 证明:f'(x0)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象与
的图象与 轴交于点
轴交于点 ,周期是
,周期是 .
.(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点
 ,点
,点 是该函数图象上一点,点
是该函数图象上一点,点 是
是 的中点,当
的中点,当 ,
,  时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为 ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 .
.(1)求椭圆
 的方程式;
的方程式;(2)已知动直线
 与椭圆
与椭圆 相交于
相交于 两点.
两点.①若线段
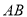 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率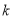 的值;
的值;②已知点
 ,求证:
,求证:  为定值.
为定值.
相关试题

