【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,
为参数, ![]() ),其中
),其中![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的直角坐标系;
交点的直角坐标系;
(Ⅱ)若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)交点坐标为![]() ,
, ![]() .(2)最大值为
.(2)最大值为![]() .
.
【解析】试题分析:(1)根据![]() 将曲线
将曲线![]() 与
与![]() 的极坐标方程化为直角坐标方程,再联立方程组求解交点的直角坐标,(2)曲线
的极坐标方程化为直角坐标方程,再联立方程组求解交点的直角坐标,(2)曲线![]() 为直线,倾斜角为
为直线,倾斜角为![]() ,极坐标方程为
,极坐标方程为![]() ,代入
,代入![]() 与
与![]() 的极坐标方程可得
的极坐标方程可得![]() 的极坐标,则
的极坐标,则![]() 为对应极径之差的绝对值,即
为对应极径之差的绝对值,即![]() ,最后根据三角函数关系有界性求最值.
,最后根据三角函数关系有界性求最值.
试题解析:解:(Ⅰ) ![]() :
: ![]() ,
, ![]() :
: ![]() ,
,
联立得交点坐标为![]() ,
, ![]() .
.
(Ⅱ)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() .
.
因此得到![]() 的极坐标为
的极坐标为![]() ,
,
![]() 的极坐为
的极坐为![]() .
.
所以![]() ,
,
当![]() 时,
时, ![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
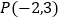 是函数
是函数 图象上的点,
图象上的点,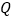 是双曲线在第四象限这一分支上的动点,过点
是双曲线在第四象限这一分支上的动点,过点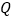 作直线,使其与双曲线
作直线,使其与双曲线 只有一个公共点,且与
只有一个公共点,且与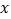 轴、
轴、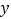 轴分别交于点
轴分别交于点 、
、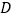 ,另一条直线
,另一条直线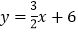 与
与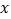 轴、
轴、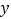 轴分别交于点
轴分别交于点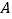 、
、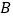 .
.则(1)
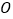 为坐标原点,三角形
为坐标原点,三角形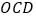 的面积为__________.
的面积为__________.(2)四边形
 面积的最小值为__________.
面积的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).

(1)分别写出两种产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=x2+(a+2)x﹣3,x∈[a,b]的图象关于直线x=1对称.
(1)求a、b的值和函数的零点
(2)当函数f(x)的定义域是[0,3]时,求函数f(x)的值域.. -
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
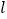 :
: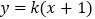 (
(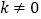 )与椭圆
)与椭圆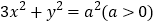 相交于
相交于 ,
,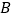 两个不同的点,与
两个不同的点,与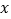 轴相交于点
轴相交于点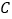 ,记
,记 为坐标原点.
为坐标原点.(1)证明:
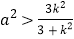 ;
;(2)若
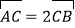 ,求
,求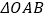 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
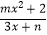 是奇函数,且f(2)=
是奇函数,且f(2)=  .
.
(1)求实数m和n的值;
(2)判断函数f(x)在(﹣∞,0)上的单调性,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有两个独立的转盘(
 )、(
)、( ).两个图中三个扇形区域的圆心角分别为
).两个图中三个扇形区域的圆心角分别为 、
、 、
、 .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘( )指针所对的数为
)指针所对的数为 ,转盘(
,转盘( )指针所对的数为
)指针所对的数为 ,(
,( 、
、 ),求下列概率:
),求下列概率:
(1)
 ;
;(2)
 .
.
相关试题

