【题目】设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 相交于
相交于![]() ,
,![]() 两个不同的点,与
两个不同的点,与![]() 轴相交于点
轴相交于点![]() ,记
,记![]() 为坐标原点.
为坐标原点.
(1)证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)设直线![]() 的方程为
的方程为![]() ,将直线的方程代入抛物线的方程,消去
,将直线的方程代入抛物线的方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,再结合直线
的一元二次方程,再结合直线![]() 与椭圆相交于两个不同的点得到根的判别式大于
与椭圆相交于两个不同的点得到根的判别式大于![]() ,从而解决问题;(2)设
,从而解决问题;(2)设![]() ,
,![]() ,由(1)得
,由(1)得![]() ,由
,由![]() ,得
,得![]() 从而求得
从而求得![]() 的面积,最后利用基本不等式求得其最大值,及取得最大值时的
的面积,最后利用基本不等式求得其最大值,及取得最大值时的![]() 值,从而即可求得
值,从而即可求得![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
试题解析:(1)依题意,直线![]() 显然不平行于坐标轴,故
显然不平行于坐标轴,故![]() 可化为
可化为![]() ,
,
将![]() 代入
代入![]() ,整理得
,整理得![]() ,①
,①
由直线![]() 与椭圆相交于两个不同的点,得
与椭圆相交于两个不同的点,得![]() ,
,
化简整理即得![]() .(*)
.(*)
(2)![]() ,
,![]() ,由①,得
,由①,得![]() ,②
,②
因为![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,③
,③
由②③联立,解得![]() ,④
,④
![]() 的面积
的面积![]()
![]() ,
,
上式取等号的条件是![]() ,即
,即![]() .
.
当![]() 时,由④解得
时,由④解得![]() ;当
;当![]() 时,由④解得
时,由④解得![]() .
.
将![]() ,
,![]() 及
及![]() ,
,![]() 这两组值分别代入①,
这两组值分别代入①,
均可解出![]() ,
,
经验证,![]() ,
,![]() 满足(*)式.
满足(*)式.
所以,![]() 的面积取得最大值时椭圆方程为
的面积取得最大值时椭圆方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).

(1)分别写出两种产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=x2+(a+2)x﹣3,x∈[a,b]的图象关于直线x=1对称.
(1)求a、b的值和函数的零点
(2)当函数f(x)的定义域是[0,3]时,求函数f(x)的值域.. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
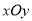 中,曲线
中,曲线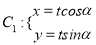 (
(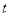 为参数,
为参数, 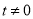 ),其中
),其中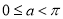 ,在以
,在以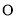 为极点,
为极点, 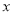 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 ,曲线
,曲线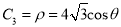 .
.(Ⅰ)求
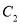 与
与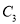 交点的直角坐标系;
交点的直角坐标系;(Ⅱ)若
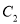 与
与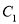 相交于点
相交于点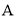 ,
,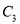 与
与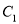 相交于点
相交于点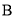 ,求
,求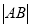 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
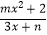 是奇函数,且f(2)=
是奇函数,且f(2)=  .
.
(1)求实数m和n的值;
(2)判断函数f(x)在(﹣∞,0)上的单调性,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有两个独立的转盘(
 )、(
)、( ).两个图中三个扇形区域的圆心角分别为
).两个图中三个扇形区域的圆心角分别为 、
、 、
、 .用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘(
.用这两个转盘进行玩游戏,规则是:依次随机转动两个转盘再随机停下(指针固定不会动,当指针恰好落在分界线时,则这次结果无效,重新开始),记转盘( )指针所对的数为
)指针所对的数为 ,转盘(
,转盘( )指针所对的数为
)指针所对的数为 ,(
,( 、
、 ),求下列概率:
),求下列概率:
(1)
 ;
;(2)
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学考试试题中共有
 道选择题,每道选择题都有
道选择题,每道选择题都有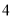 个选项,其中仅有一个是正确的.评分标准规定:“每题只选
个选项,其中仅有一个是正确的.评分标准规定:“每题只选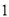 项,答对得
项,答对得 分,不答或答错得
分,不答或答错得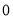 分.”某考生每道题都给了一个答案,已确定有
分.”某考生每道题都给了一个答案,已确定有 道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:(Ⅰ)得
 分的概率;
分的概率;(Ⅱ)所得分数
 的数学期望.
的数学期望.
相关试题

