【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
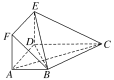
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
参考答案:
【答案】见解析
【解析】解:(1)证明:因为AD=1,CD=2,AC=![]() ,
,
所以AD2+CD2=AC2,
所以△ADC为直角三角形,且AD⊥DC.
同理,因为ED=1,CD=2,EC=![]() ,
,
所以ED2+CD2=EC2,
所以△EDC为直角三角形,且ED⊥DC.
又四边形ADEF是正方形,所以AD⊥DE,
又AD∩DC=D,所以ED⊥平面ABCD.
又BC平面ABCD,所以ED⊥BC.
在梯形ABCD中,过点B作BH⊥CD于点H,

故四边形ABHD是正方形,所以∠ADB=45°,BD=![]() 。
。
在Rt△BCH中,BH=CH=1,所以BC=![]() ,
,
故BD2+BC2=DC2,所以BC⊥BD.
因为BD∩ED=D,BD平面EBD,ED平面EBD,
所以BC⊥平面EBD,
又BC平面EBC,所以平面EBC⊥平面EBD.
(2)在线段BC上存在一点T,使得MT∥平面BDE,此时3BT=BC.
连接MT,在△EBC中,因为![]() =
=![]() =
=![]() ,所以MT∥EB.
,所以MT∥EB.
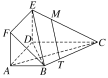
又MT平面BDE,EB平面BDE,
所以MT∥平面BDE。
-
科目: 来源: 题型:
查看答案和解析>>【题目】吉安一中举行了一次“环保知识竞赛”活动,为了解本了次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为
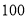 分)作为样本(样本容量为
分)作为样本(样本容量为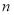 )进行统计. 按照
)进行统计. 按照 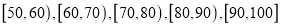 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在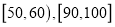 的数据).
的数据).(1)求样本容量
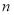 和频率分布直方图中的
和频率分布直方图中的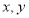 的值;
的值; (2)在选取的样本中,从竞赛学生成绩是
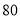 分以上(含
分以上(含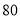 分)的同学中随机抽取
分)的同学中随机抽取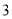 名同学到市政广场参加环保知识宣传的志愿者活动,设
名同学到市政广场参加环保知识宣传的志愿者活动,设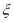 表示所抽取的
表示所抽取的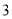 名同学中得分在
名同学中得分在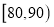 的学生人数,求
的学生人数,求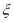 的分布列及数学期望.
的分布列及数学期望.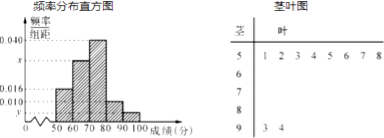
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方体ABCDA1B1C1D1中,AB=AA1=1,E为BC中点.
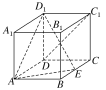
(1)求证:C1D⊥D1E;
(2)在棱AA1上是否存在一点M,使得BM∥平面AD1E?若存在,求
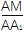 的值,若不存在,说明理由;
的值,若不存在,说明理由;(3)若二面角B1AED1的大小为90°,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
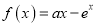 ,
, 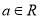 ,
, 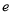 为自然对数的底数.
为自然对数的底数.(Ⅰ)若函数
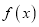 存在两个零点,求
存在两个零点,求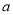 的取值范围;
的取值范围;(Ⅱ)若对任意
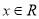 ,
, 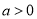 ,
, 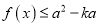 恒成立,求实数
恒成立,求实数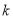 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某市的高一学生中随机抽取400名同学的体重进行统计,得到如图所示频率分布直方图.
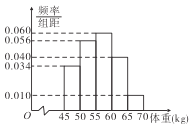
(Ⅰ)估计从该市高一学生中随机抽取一人,体重超过
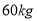 的概率;
的概率;(Ⅱ)假设该市高一学生的体重
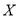 服从正态分布
服从正态分布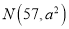 .
.(ⅰ)利用(Ⅰ)的结论估计该高一某个学生体重介于
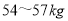 之间的概率;
之间的概率;(ⅱ)从该市高一学生中随机抽取3人,记体重介于
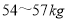 之间的人数为
之间的人数为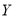 ,利用(ⅰ)的结论,求
,利用(ⅰ)的结论,求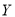 的分布列及
的分布列及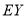 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在区间
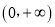 上的函数
上的函数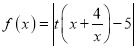 ,其中常数
,其中常数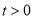 .
.(1)若函数
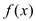 分别在区间
分别在区间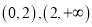 上单调,试求
上单调,试求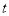 的取值范围;
的取值范围;(2)当
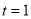 时,方程
时,方程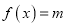 有四个不相等的实根
有四个不相等的实根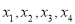 .
.①证明:
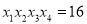 ;
;②是否存在实数
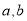 ,使得函数
,使得函数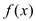 在区间
在区间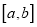 单调,且
单调,且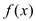 的取值范围为
的取值范围为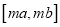 ,若存在,求出
,若存在,求出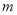 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
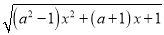 ;
;(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
相关试题

