【题目】已知定义在区间![]() 上的函数
上的函数![]() ,其中常数
,其中常数![]() .
.
(1)若函数![]() 分别在区间
分别在区间![]() 上单调,试求
上单调,试求![]() 的取值范围;
的取值范围;
(2)当![]() 时,方程
时,方程![]() 有四个不相等的实根
有四个不相等的实根![]() .
.
①证明: ![]() ;
;
②是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 单调,且
单调,且![]() 的取值范围为
的取值范围为![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(1) ![]() (2)见解析,
(2)见解析, ![]()
【解析】试题分析:(1)结合对勾函数的特征,即可知![]() ,从而求出参数范围;(2)当
,从而求出参数范围;(2)当![]() 时,方程
时,方程![]() 即为
即为![]() 或
或![]() ,由韦达定理可证明.结合函数图像及其单调性,分类讨论分别在四个单调区间内去求解,最后求并集即可.
,由韦达定理可证明.结合函数图像及其单调性,分类讨论分别在四个单调区间内去求解,最后求并集即可.
试题解析:(1)设![]()
∵![]() ∴函数
∴函数![]() 分别在区间
分别在区间![]() 上单调 且
上单调 且![]()
要使函数![]() 分别在区间
分别在区间![]() 上单调
上单调
则只需![]()
(2)①当![]() 时,
时, ![]() 或
或![]()
即![]() 或
或![]()
∵![]() 为方程
为方程![]() 的四个不相等的实根
的四个不相等的实根
∴由根与系数的关系得![]()
②如图,可知![]() ,
, ![]() 在
在![]() 、
、![]() 、
、![]() 、
、![]() 均为单调函数
均为单调函数
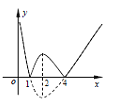
(Ⅰ)当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
则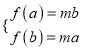 两式相除整理得
两式相除整理得![]()
∵![]() ∴上式不成立 即
∴上式不成立 即![]() 无解,
无解, ![]() 无取值 10分
无取值 10分
(Ⅱ)当![]() 时,
时, ![]() 在
在![]() 上单调递增
上单调递增
则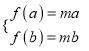 即
即![]() 在
在![]() 有两个不等实根
有两个不等实根
而令![]() 则
则![]()
作![]() 在
在![]() 的图像可知,
的图像可知, ![]() 12分
12分
(Ⅲ)当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
则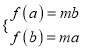 两式相除整理得
两式相除整理得![]()
∴![]() ∴
∴![]() ∴
∴![]()
由![]() 得
得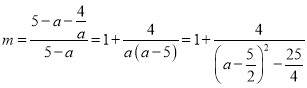
则![]() 关于
关于![]() 的函数是单调的,而
的函数是单调的,而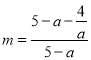 应有两个不同的解
应有两个不同的解
∴此种情况无解
(Ⅳ)当![]() 时,同(Ⅰ)可以解得
时,同(Ⅰ)可以解得![]() 无取值
无取值
综上, ![]() 的取值范围为
的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
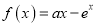 ,
, 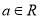 ,
, 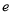 为自然对数的底数.
为自然对数的底数.(Ⅰ)若函数
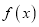 存在两个零点,求
存在两个零点,求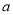 的取值范围;
的取值范围;(Ⅱ)若对任意
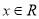 ,
, 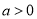 ,
, 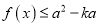 恒成立,求实数
恒成立,求实数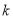 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=
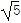 。
。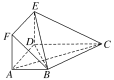
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某市的高一学生中随机抽取400名同学的体重进行统计,得到如图所示频率分布直方图.
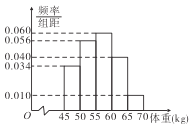
(Ⅰ)估计从该市高一学生中随机抽取一人,体重超过
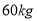 的概率;
的概率;(Ⅱ)假设该市高一学生的体重
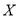 服从正态分布
服从正态分布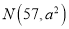 .
.(ⅰ)利用(Ⅰ)的结论估计该高一某个学生体重介于
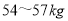 之间的概率;
之间的概率;(ⅱ)从该市高一学生中随机抽取3人,记体重介于
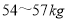 之间的人数为
之间的人数为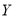 ,利用(ⅰ)的结论,求
,利用(ⅰ)的结论,求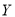 的分布列及
的分布列及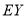 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
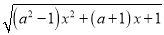 ;
;(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知直线
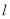 的参数方程为
的参数方程为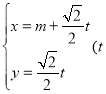 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,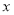 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线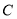 的极坐标方程为
的极坐标方程为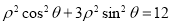 .且曲线
.且曲线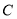 的左焦点
的左焦点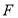 在直线
在直线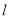 上.
上.(1)若直线
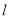 与曲线
与曲线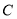 交于
交于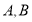 两点,求
两点,求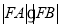 的值;
的值;(2)求曲线
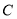 的内接矩形的周长的最大值.
的内接矩形的周长的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
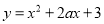 ,
, 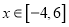 .
.(1)若
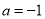 ,写出函数的单调增区间和减区间;
,写出函数的单调增区间和减区间;(2)若
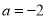 ,求函数的最大值和最小值;
,求函数的最大值和最小值;(3)若函数在
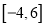 上是单调函数,求实数
上是单调函数,求实数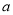 的取值范围.
的取值范围.
相关试题

