【题目】已知函数f(x)=lnx+bx﹣c,f(x)在点(1,f(1))处的切线方程为x+y+4=0.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)若在区间 ![]() 内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
内,恒有f(x)≥2lnx+kx成立,求k的取值范围.
参考答案:
【答案】
(1)解:由题意,f′(x)= ![]() +b,则f′(1)=1+b,
+b,则f′(1)=1+b,
∵在点(1,f(1))处的切线方程为x+y+4=0,
∴切线斜率为﹣1,则1+b=﹣1,得b=﹣2,
将(1,f(1))代入方程x+y+4=0,
得:1+f(1)+4=0,解得f(1)=﹣5,
∴f(1)=b﹣c=﹣5,将b=2代入得c=3,
故f(x)=lnx﹣2x﹣3
(2)解:依题意知函数的定义域是(0,+∞),且f′(x)= ![]() ﹣2,
﹣2,
令f′(x)>0得,0<x< ![]() ,令f′(x)<0得,x>
,令f′(x)<0得,x> ![]() ,
,
故f(x)的单调增区间为(0, ![]() ),单调减区间为(
),单调减区间为( ![]() ,+∞)
,+∞)
(3)解:由f(x)≥2lnx+kx,k≤﹣2﹣ ![]() 在区间
在区间 ![]() 内恒成立,
内恒成立,
设g(x)=﹣2﹣ ![]() ,则g′(x)=
,则g′(x)= ![]() ,
,
∴g(x)在区间 ![]() 上单调递增,
上单调递增,
∴g(x)的最小值为g( ![]() )=2ln2﹣8,
)=2ln2﹣8,
∴k≤2ln2﹣8
【解析】(1)由求导公式、法则求出f′(x),根据题意和导数的几何意义求出b的值,将(1,f(1))代入方程x+y+4=0求出f(1),代入解析式列出方程求出c,即可求出函数f(x)的解析式;(2)由(1)求出函数的定义域和f′(x),求出f′(x)>0和f′(x)<0的解集,即可求出函数f(x)的单调区间;(3)由f(x)≥2lnx+kx,k≤﹣2﹣ ![]() 在区间
在区间 ![]() 内恒成立,求出右边的最小值,即可得出结论.
内恒成立,求出右边的最小值,即可得出结论.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案
不善于使用学案
总计
学习成绩优秀
40
学习成绩一般
30
总计
100
参考公式:
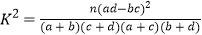 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:P(K2≥k0)
0.050
0.010
0.001
k0
3.841
6.635
10.828
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的对称轴为坐标轴,顶点是坐标原点,准线方程为x=﹣1,直线l与抛物线相交于不同的A,B两点.
(1)求抛物线的标准方程;
(2)如果直线l过抛物线的焦点,求 的值;
的值;
(3)如果 ,直线l是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
,直线l是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A. “至少有一个黑球”与“都是红球”
B. “至少有一个黑球”与“至少有一个红球”
C. “至少有一个黑球”与“都是黑球”
D. “恰有一个黑球”与“恰有两个黑球”
-
科目: 来源: 题型:
查看答案和解析>>【题目】将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的编号为003.这600名学生分住在3个营区,从001到300住在第1营区,从301到495住在第2营区,从496到600住在第3营区,则3个营区被抽中的人数依次为( )
A. 26,16,8 B. 25,16,9
C. 25,17,8 D. 24,17,9
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为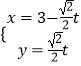 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-5:不等式选讲]
已知函数f(x)=|x﹣m|﹣1.
(1)若不等式f(x)≤2的解集为{x|﹣1≤x≤5},求实数m的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥t﹣2对一切实数x恒成立,求实数t的取值范围.
相关试题

