【题目】某企业一天中不同时刻的用电量![]() (万千瓦时)关于时间
(万千瓦时)关于时间![]() (单位:小时,其中
(单位:小时,其中![]() 对应凌晨0点)的函数
对应凌晨0点)的函数![]() 近似满足
近似满足![]()
![]() ,如图是函数
,如图是函数![]() 的部分图象.
的部分图象.

(1)求![]() 的解析式;
的解析式;
(2)已知该企业某天前半日能分配到的供电量![]() (万千瓦时)与时间
(万千瓦时)与时间![]() (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型![]() 模拟,当供电量
模拟,当供电量![]() 小于企业用电量
小于企业用电量![]() 时,企业必须停产.初步预计开始停产的临界时间
时,企业必须停产.初步预计开始停产的临界时间![]() 在中午11点到12点之间,用二分法估算
在中午11点到12点之间,用二分法估算![]() 所在的一个区间(区间长度精确到15分钟).
所在的一个区间(区间长度精确到15分钟).
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由图象,利用最大值与最小值差的一半求得![]() ,由最大值与最小值和的一半求得
,由最大值与最小值和的一半求得![]() ,由周期求得
,由周期求得![]() ,由特殊点求得
,由特殊点求得![]() 的值,从而可得
的值,从而可得![]() 的解析式; (2)构造函数
的解析式; (2)构造函数![]() ,先判断
,先判断![]() 在
在![]() 上是单调递增函数,再利用二分法判断函数
上是单调递增函数,再利用二分法判断函数![]() 的零点所在的区间.
的零点所在的区间.
(1)由图象可知A=![]() =
=![]() ,B=
,B=![]() =2,T=12=
=2,T=12=![]() ,ω=
,ω=![]() ,
,
代入点(0,2.5)得sinφ=1,
∵0<φ<π,∴φ=![]() ;
;
综上,A=![]() ,B=2,ω=
,B=2,ω=![]() ,φ=
,φ=![]() ,
,
即f(t)=![]() sin(
sin(![]() t+
t+![]() )+2.
)+2.
(2)由(1)知f(t)=![]() sin(
sin(![]() t+
t+![]() )+2=
)+2=![]() cos
cos![]() t+2,
t+2,
令h(t)=f(t)-g(t),
设h(t0)=0,则t0为该企业的开始停产的临界时间;
易知h(t)在(11,12)上是单调递增函数;
由h(11)=f(11)-g(11)=![]() cos
cos![]() +2+2×11-25=
+2+2×11-25=![]() -1<0,
-1<0,
h(12)=f(12)-g(12)=![]() cos
cos![]() +2+2×12-25=
+2+2×12-25=![]() >0,
>0,
又h(11.5)=f(11.5)-g(11.5)=![]() cos
cos![]() +2+2×11.5-25=
+2+2×11.5-25=![]() cos(-
cos(-![]() )=
)=![]() cos
cos![]() =
=![]() >0,
>0,
则t0∈(11,11.5),即11点到11点30分之间(大于15分钟),
又h(11.25)=f(11.25)-g(11.25)=![]() cos
cos![]() +2+2×11.25-25<
+2+2×11.25-25<![]() ×1-0.5=0,
×1-0.5=0,
则t0∈(11.25,11.5),即11点15分到11点30分之间(正好15分钟).
所以,企业开始停产的临界时间t0所在的区间为(11.25,11.5).
-
科目: 来源: 题型:
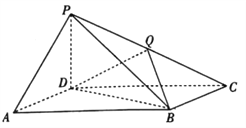
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为平行四边形,
为平行四边形,  ,
,  ,且
,且 底面
底面 .
.
(1)证明:平面
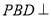 平面
平面 ;
;(2)若
 为
为 的中点,且
的中点,且 ,求二面角
,求二面角 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】过点(
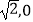 )引直线l与曲线y=
)引直线l与曲线y= 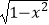 相交于A,B两点,O为坐标原点,当△ABO的面积取得最大值时,直线l的斜率等于( )
相交于A,B两点,O为坐标原点,当△ABO的面积取得最大值时,直线l的斜率等于( )
A.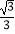
B.-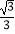
C.
D.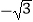
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】动圆M与定圆C:x2+y2+4x=0相外切,且与直线l:x-2=0相切,则动圆M的圆心的轨迹方程为( )
A. y2-12x+12=0 B. y2+12x-12=0
C. y2+8x=0 D. y2-8x=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
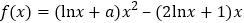 .
.(1)当
 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)若函数
 的图象与
的图象与 轴有且仅有一个交点,求实数
轴有且仅有一个交点,求实数 的值;
的值;(3)在(2)的条件下,对任意的
 ,均有
,均有 成立,求正实数
成立,求正实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,圆C的参数方程
 (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+
 )=3
)=3 ,射线OM:θ=
,射线OM:θ= 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
相关试题

