【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
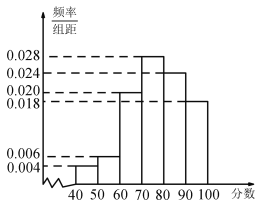
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
参考答案:
【答案】(1)![]() ;77.14;(2)
;77.14;(2)![]() .
.
【解析】
(1)由题意列出频率分布表,求和即可估计该地区用户对该电讯企业评分不低于70分的概率;利用中位数两侧的概率和相等列方程即可估计对该电讯企业评分的中位数;
(2)由题意计算出受调查用户评分在![]() 、
、![]() 的人数,求出总的基本事件个数及满足要求的基本事件的个数,由古典概型概率公式即可得解.
的人数,求出总的基本事件个数及满足要求的基本事件的个数,由古典概型概率公式即可得解.
(1)由题意,该地区用户对该电讯企业评分的频率分布如下表:
评分 |
|
|
|
|
|
|
频率 | 0.04 | 0.06 | 0.20 | 0.28 | 0.24 | 0.18 |
因此可估计评分不低于70分的概率为![]() ;
;
对该电讯企业评分的中位数设为x,可得![]() ,
,
则![]() ,
,
解得![]() ,
,
所以可估计对该电讯企业评分的中位数为![]() ;
;
(2)受调查用户评分在![]() 的有
的有![]() 人,
人,
若编号依次为1,2,3,4,从中选2人的事件有![]() 、
、
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,
共有![]() 个基本事件;
个基本事件;
受调查用户评分在![]() 的有
的有![]() 人,
人,
若编号依次为1,2,3,..9,10,从中选2人,
可得共有![]() 个基本事件;
个基本事件;
因此2人评分都在![]() 的概率
的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】焦点在x轴上的椭圆C:
 经过点
经过点 ,椭圆C的离心率为
,椭圆C的离心率为 .
. ,
, 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.(1)求椭圆的标准方程;
(2)若点M为
 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数 ,使得
,使得 ;若存在,请求出
;若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
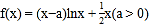 .
.(1)若
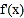 是
是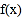 的导函数,讨论
的导函数,讨论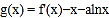 的单调性;
的单调性;(2)若
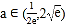 (
(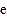 是自然对数的底数),求证:
是自然对数的底数),求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
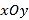 中,直线
中,直线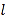 的参数方程为
的参数方程为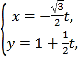 (
(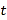 为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线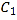 的方程为
的方程为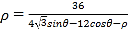 ,定点
,定点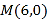 ,点
,点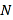 是曲线
是曲线 上的动点,
上的动点, 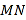 为
为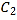 的中点.
的中点.(1)求点
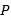 的轨迹
的轨迹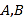 的直角坐标方程;
的直角坐标方程;(2)已知直线
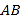 与
与 轴的交点为
轴的交点为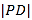 ,与曲线
,与曲线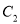 的交点为
的交点为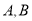 ,若
,若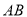 的中点为
的中点为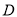 ,求
,求 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】焦点在x轴上的椭圆C:
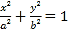 经过点
经过点 ,椭圆C的离心率为
,椭圆C的离心率为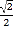 .
.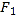 ,
,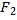 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.(1)求椭圆的标准方程;
(2)若点M为
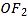 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数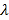 ,使得
,使得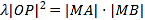 ;若存在,请求出
;若存在,请求出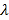 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
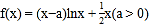 .
.(1)若
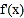 是
是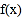 的导函数,讨论
的导函数,讨论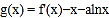 的单调性;
的单调性;(2)若
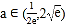 (
(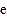 是自然对数的底数),求证:
是自然对数的底数),求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
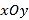 中,直线
中,直线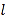 的参数方程为
的参数方程为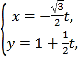 (
(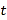 为参数),以原点为极点,
为参数),以原点为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线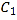 的方程为
的方程为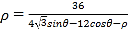 ,定点
,定点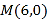 ,点
,点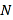 是曲线
是曲线 上的动点,
上的动点, 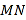 为
为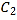 的中点.
的中点.(1)求点
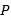 的轨迹
的轨迹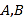 的直角坐标方程;
的直角坐标方程;(2)已知直线
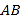 与
与 轴的交点为
轴的交点为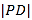 ,与曲线
,与曲线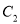 的交点为
的交点为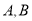 ,若
,若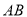 的中点为
的中点为 ,求
,求 的长.
的长.
相关试题

