【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)存在
(2)存在![]() 满足条件,详见解析
满足条件,详见解析
【解析】
(1)根据所给条件列出方程组,求解即可。
(2)对直线的斜率存在与否分类讨论,当斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,联立直线与椭圆方程,利用韦达定理,即可表示出
,联立直线与椭圆方程,利用韦达定理,即可表示出![]() 、
、![]() 、
、![]() ,则
,则![]() 可求。
可求。
解:(1)由已知可得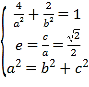 ,解得
,解得![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)若直线的斜率不存在时,![]() ,
,![]() ,
,
所以![]() ;
;
当斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
联立直线![]() 与椭圆方程
与椭圆方程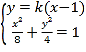 ,消去y,得
,消去y,得![]() ,
,
所以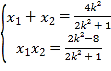 .
.
因为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
联立直线![]() 与椭圆方程
与椭圆方程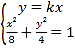 ,消去
,消去![]() ,得
,得![]() ,解得
,解得![]() .
.
![]() ,
,
![]() ,
,
同理![]() ,
,![]() ,
,
因为![]() ,
,
![]() ,故
,故![]() ,存在
,存在![]() 满足条件,
满足条件,
综上可得,存在![]() 满足条件.
满足条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(Ⅰ)当曲线
 在点
在点 处的切线与直线
处的切线与直线 垂直时,求
垂直时,求 的值;
的值;(Ⅱ)若函数
 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
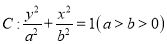 的上下两个焦点分别为
的上下两个焦点分别为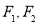 ,过点
,过点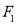 与
与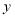 轴垂直的直线交椭圆
轴垂直的直线交椭圆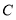 于
于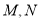 两点,
两点,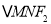 的面积为
的面积为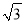 ,椭圆
,椭圆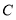 的长轴长是短轴长的
的长轴长是短轴长的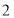 倍.
倍.(1)求椭圆
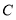 的标准方程;
的标准方程;(2)已知
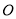 为坐标原点,直线
为坐标原点,直线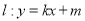 与
与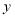 轴交于点
轴交于点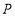 ,与椭园
,与椭园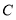 交于
交于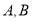 两个不同的点,若存在实数
两个不同的点,若存在实数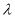 ,使得
,使得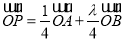 ,求
,求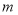 的取值范围,
的取值范围, -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (
( )与双曲线
)与双曲线 (
( ,
, )有相同的焦点
)有相同的焦点 ,点
,点 是两条曲线的一个交点,且
是两条曲线的一个交点,且 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】汕头某家电企业要将刚刚生产的100台变频空调送往市内某商场,现有4辆甲型货车和8辆乙型货车可供调配,每辆甲型货车的运输费用是400元,可装空调20台,每辆乙型货车的运输费用是300元,可装空调10台,若每辆车至多运一次,则企业所花的最少运费为( )
A. 2000元B. 2200元C. 2400元D. 2800元
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌新款夏装即将上市,为了对新款夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
连锁店
A店
B店
C店
售价x(元)
80
86
82
88
84
90
销量y(元)
88
78
85
75
82
66
(1)分别以三家连锁店的平均售价与平均销量为散点,如A店对应的散点为
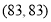 ,求出售价与销量的回归直线方程
,求出售价与销量的回归直线方程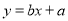 ;
;(2)在大量投入市场后,销量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该新夏装在销售上获得最大利润,该款夏装的单价应定为多少元?(保留整数)
附:
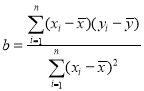 ,
,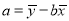 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在
 ,
, ,
, ,
, ,
, ,
,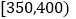 (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为
 ,
, 的芒果中随机抽取
的芒果中随机抽取 个,再从这
个,再从这 个中随机抽取
个中随机抽取 个,求这
个,求这 个芒果中恰有
个芒果中恰有 个在
个在 内的概率.
内的概率.(3)某经销商来收购芒果,以各组数据的中间数代表这组数据的平均值,用样本估计总体,该种植园中还未摘下的芒果大约还有
 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:A:所以芒果以
 元/千克收购;
元/千克收购;B:对质量低于
 克的芒果以
克的芒果以 元/个收购,高于或等于
元/个收购,高于或等于 克的以
克的以 元/个收购.
元/个收购.通过计算确定种植园选择哪种方案获利更多?
相关试题

