【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为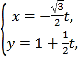 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() ,定点
,定点![]() ,点
,点![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为
为![]() 的中点.
的中点.
(1)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,若
,若![]() 的中点为
的中点为![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)求出曲线C1的直角坐标方程为![]() ,设点N(x′,y′),Q(x,y),由中点坐标公式得
,设点N(x′,y′),Q(x,y),由中点坐标公式得![]() ,由此能求出点Q的轨迹C2的直角坐标方程.(2)
,由此能求出点Q的轨迹C2的直角坐标方程.(2)![]() 的坐标为
的坐标为![]() ,设
,设![]() 的参数方程为
的参数方程为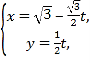 ,(
,( ![]() 为参数)代入曲线
为参数)代入曲线![]() 的直角坐标方程得
的直角坐标方程得![]() ,根据韦达定理,利用t的参数意义得
,根据韦达定理,利用t的参数意义得![]()
即可得解.
试题解析:
(1)由题意知,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
设点![]() ,
, ![]() ,由中点坐标公式得
,由中点坐标公式得![]() ,
,
代入![]() 中,得点
中,得点![]() 的轨迹
的轨迹![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)![]() 的坐标为
的坐标为![]() ,设
,设![]() 的参数方程为
的参数方程为 ,(
,( ![]() 为参数)代入曲线
为参数)代入曲线![]() 的直角坐标方程得:
的直角坐标方程得: ![]() ,
,
设点![]() 对应的参数分别为
对应的参数分别为![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
-
科目: 来源: 题型:
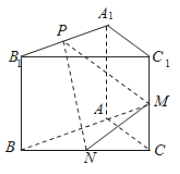
查看答案和解析>>【题目】如图,已知三棱柱
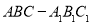 中,侧棱与底面垂直,且
中,侧棱与底面垂直,且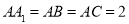 ,
,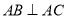 ,
,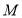 、
、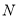 分别是
分别是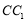 、
、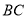 的中点,点
的中点,点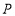 在线段
在线段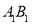 上,且
上,且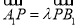 .
.
(1)求证:不论
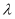 取何值,总有
取何值,总有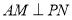 ;
;(2)当
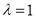 时,求平面
时,求平面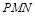 与平面
与平面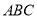 所成二面角的余弦值.
所成二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】焦点在x轴上的椭圆C:
 经过点
经过点 ,椭圆C的离心率为
,椭圆C的离心率为 .
. ,
, 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.(1)求椭圆的标准方程;
(2)若点M为
 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数 ,使得
,使得 ;若存在,请求出
;若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
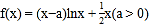 .
.(1)若
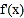 是
是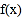 的导函数,讨论
的导函数,讨论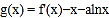 的单调性;
的单调性;(2)若
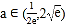 (
(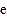 是自然对数的底数),求证:
是自然对数的底数),求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为
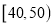 ,
,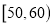 ,……
,……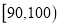 .
.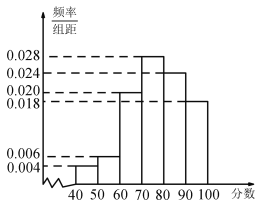
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在
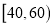 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在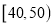 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】焦点在x轴上的椭圆C:
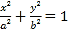 经过点
经过点 ,椭圆C的离心率为
,椭圆C的离心率为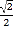 .
.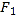 ,
,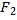 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.(1)求椭圆的标准方程;
(2)若点M为
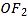 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数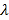 ,使得
,使得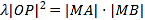 ;若存在,请求出
;若存在,请求出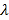 的值,若不存在,请说明理由.
的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
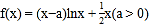 .
.(1)若
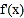 是
是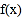 的导函数,讨论
的导函数,讨论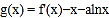 的单调性;
的单调性;(2)若
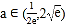 (
(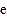 是自然对数的底数),求证:
是自然对数的底数),求证: .
.
相关试题

