【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() 均为正的常数)的最小正周期为
均为正的常数)的最小正周期为![]() ,当
,当![]() 时,函数
时,函数![]() 取得最小值,则下列结论正确的是( )
取得最小值,则下列结论正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】
依题意可求ω=2,又当x![]() 时,函数f(x)取得最小值,可解得φ,从而可求解析式f(x)=Asin(2x
时,函数f(x)取得最小值,可解得φ,从而可求解析式f(x)=Asin(2x![]() ),利用正弦函数的图象和性质及诱导公式即可比较大小.
),利用正弦函数的图象和性质及诱导公式即可比较大小.
解:依题意得,函数f(x)的周期为π,
∵ω>0,
∴ω![]() 2.
2.
又∵当x![]() 时,函数f(x)取得最小值,
时,函数f(x)取得最小值,
∴2![]() φ=2kπ
φ=2kπ![]() ,k∈Z,可解得:φ=2kπ
,k∈Z,可解得:φ=2kπ![]() ,k∈Z,
,k∈Z,
∴f(x)=Asin(2x+2kπ![]() )=Asin(2x
)=Asin(2x![]() ).
).
∴f(﹣2)=Asin(﹣4![]() )=Asin(
)=Asin(![]() 4+2π)>0.
4+2π)>0.
f(2)=Asin(4![]() )<0,
)<0,
f(0)=Asin![]() Asin
Asin![]() 0,
0,
又∵![]() 4+2π
4+2π![]() ,而f(x)=Asinx在区间(
,而f(x)=Asinx在区间(![]() ,
,![]() )是单调递减的,
)是单调递减的,
∴f(2)<f(﹣2)<f(0).
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明你的结论;
(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数
 的图象向左平移1个单位,再将图象上的所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数
的图象向左平移1个单位,再将图象上的所有点的纵坐标伸长到原来的2倍(横坐标不变),得到函数 的图象.
的图象.(1)求函数
 的解析式和定义域;
的解析式和定义域;(2)求函数
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=tan(ωx+φ)(ω>0,0<φ<
 ),已知函数y=f(x)的图象与x轴相邻两个交点的距离为
),已知函数y=f(x)的图象与x轴相邻两个交点的距离为 ,且图象关于点M(-
,且图象关于点M(- ,0)对称.
,0)对称.(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)求不等式-1≤f(x)≤
 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,任取
,任取 ,若函数
,若函数 在区间
在区间 上的最大值为
上的最大值为 ,最小值为
,最小值为 ,记
,记 .
.(1)求函数
 的最小正周期及对称轴方程;
的最小正周期及对称轴方程;(2)当
 时,求函数
时,求函数 的解析式;
的解析式;(3)设函数
 ,
, ,其中
,其中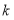 为参数,且满足关于
为参数,且满足关于 的不等式
的不等式 有解,若对任意
有解,若对任意 ,存在
,存在 ,使得
,使得 成立,求实数
成立,求实数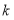 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代第一部数学专著,成于公元一世纪左右,系统总结了战国、秦、汉时期的数学成就.其中《方田》一章中记载了计算弧田(弧田就是由圆弧和其所对弦所围成弓形)的面积所用的经验公式:弧田面积=
 (弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为
(弦×矢+矢×矢),公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.现有圆心角为 ,弦长为
,弦长为 的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中
的弧田.其实际面积与按照上述经验公式计算出弧田的面积之间的误差为( )平方米.(其中 ,
, )
)A. 15 B. 16 C. 17 D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点为
的焦点为 ,准线为
,准线为 ,
, 是
是 上一点,直线
上一点,直线 与抛物线交于
与抛物线交于 两点,若
两点,若 ,则
,则 ( )
( )A.
 B. 8 C. 16 D.
B. 8 C. 16 D. 
相关试题

