【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论函数![]() 的单调性.
的单调性.
(Ⅱ)是否存在实数![]() ,使
,使![]() 对任意
对任意![]() 恒成立?若存在,试求出
恒成立?若存在,试求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】试题分析:
(Ⅰ)求出导函数![]() ,求出
,求出![]() 的解,在定义域内的各区间可得
的解,在定义域内的各区间可得![]() 的正负,即得
的正负,即得![]() 的单调区间;
的单调区间;
(Ⅱ)观察函数![]() 得
得![]() ,因此有
,因此有![]() ,这样不等式
,这样不等式![]() 可化为
可化为![]() ,设
,设![]() ,利用导数
,利用导数![]() 研究出
研究出![]() 的单调性,可根据
的单调性,可根据![]() 的取值分类讨论求只有
的取值分类讨论求只有![]() 时,可得
时,可得![]() 有最小值,由最小值
有最小值,由最小值![]()
![]() ,把这个式子作为
,把这个式子作为![]() 的函数
的函数![]() ,由导函数
,由导函数![]() 得其最大值为
得其最大值为![]() ,且
,且![]() ,从而可得
,从而可得![]() (一方面
(一方面![]() ,另一方面
,另一方面![]() ,因此只有
,因此只有![]() ),
),![]() ,再研究在
,再研究在![]() 时,
时, ![]() 是否恒成立即可.
是否恒成立即可.
试题解析:
(Ⅰ)![]() ,令
,令![]() 得
得![]() .
.
当![]() 且
且![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)注意到![]() ,则
,则![]() ,
, ![]() ①.
①.
于是, ![]() 即
即![]() ,记
,记![]() ,
, ![]() ,
,
若![]() ,则
,则![]() ,得
,得![]() 在
在![]() 上单调递减,则当
上单调递减,则当![]() 时,有
时,有![]() ,不合题意;
,不合题意;
若![]() ,易知
,易知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
得![]() 在
在![]() 上的最小值
上的最小值![]() .
.
记![]() ,则
,则![]() ,得
,得![]() 有最大值
有最大值![]() ,即
,即![]() ,
,
又![]() ,故
,故![]() ,代入①得
,代入①得![]() .
.
当![]() 时,
时, ![]() 即
即![]()
![]()
![]() .
.
记![]() ,则
,则![]() ,得
,得![]() 在
在![]() 上有最小值
上有最小值![]() ,即
,即![]() ,符合题意.
,符合题意.
综上,存在![]() ,使
,使![]() 对任意
对任意![]() 恒成立.
恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量
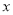 分布在
分布在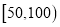 内,且销售量
内,且销售量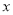 的分布频率
的分布频率 .
.(Ⅰ)求
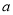 的值并估计销售量的平均数;
的值并估计销售量的平均数;(Ⅱ)若销售量大于等于70,则称该日畅销,其余为滞销.在畅销日中用分层抽样的方法随机抽取8天,再从这8天中随机抽取3天进行统计,设这3天来自
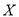 个组,求随机变量
个组,求随机变量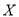 的分布列及数学期望(将频率视为概率).
的分布列及数学期望(将频率视为概率). -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在空间直角坐标系
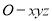 中,正四面体(各条棱均相等的三棱锥)
中,正四面体(各条棱均相等的三棱锥)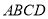 的顶点
的顶点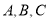 分别在
分别在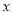 轴,
轴, 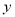 轴,
轴, 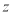 轴上.
轴上.
(Ⅰ)求证:
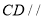 平面
平面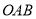 ;
;(Ⅱ)求二面角
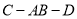 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系
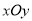 中,直线
中,直线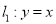 与直线
与直线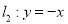 之间的阴影部分即为
之间的阴影部分即为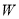 ,区域
,区域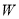 中动点
中动点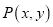 到
到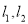 的距离之积为1.
的距离之积为1.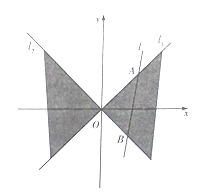
(Ⅰ)求点
 的轨迹
的轨迹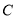 的方程;
的方程;(Ⅱ)动直线
 穿过区域
穿过区域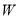 ,分别交直线
,分别交直线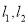 于
于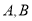 两点,若直线
两点,若直线 与轨迹
与轨迹 有且只有一个公共点,求证:
有且只有一个公共点,求证: 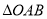 的面积恒为定值.
的面积恒为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量
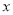 分布在
分布在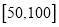 内,且销售量
内,且销售量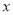 的分布频率
的分布频率 .
.(Ⅰ)求
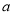 的值.
的值.(Ⅱ)若销售量大于等于80,则称该日畅销,其余为滞销,根据是否畅销从这50天中用分层抽样的方法随机抽取5天,再从这5天中随机抽取2天,求这2天中恰有1天是畅销日的概率(将频率视为概率).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在四棱锥
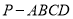 中,平面
中,平面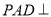 平面
平面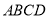 ,且
,且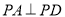 ,
, 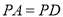 ,
, 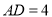 ,
, 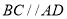 ,
, 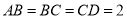 ,
,  为
为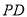 的中点.
的中点.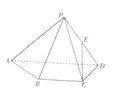
(Ⅰ)证明:
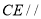 平面
平面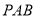 ;
;(Ⅱ)求三棱锥
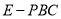 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系
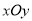 中,直线
中,直线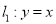 与直线
与直线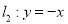 之间的阴影部分即为
之间的阴影部分即为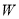 ,区域
,区域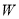 中动点
中动点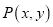 到
到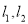 的距离之积为1.
的距离之积为1.
(Ⅰ)求点
 的轨迹
的轨迹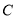 的方程;
的方程;(Ⅱ)动直线
 穿过区域
穿过区域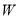 ,分别交直线
,分别交直线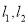 于
于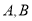 两点,若直线
两点,若直线 与轨迹
与轨迹 有且只有一个公共点,求证:
有且只有一个公共点,求证: 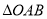 的面积恒为定值.
的面积恒为定值.
相关试题

