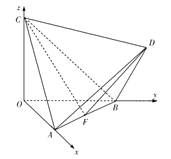
【题目】如下图,在空间直角坐标系![]() 中,正四面体(各条棱均相等的三棱锥)
中,正四面体(各条棱均相等的三棱锥)![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴上.
轴上.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)设![]() ,写出A,B,C的坐标,再求出D点坐标,从而得
,写出A,B,C的坐标,再求出D点坐标,从而得![]() 的坐标,只要它与平面
的坐标,只要它与平面![]() 的法向量垂直,即可证明线面平行;
的法向量垂直,即可证明线面平行;
(Ⅱ)求二面角,可取AB的中点F,由能证明∠CFD是所求二面角的平面角,在![]() 中由得余弦定理可得余弦值.也可求出二面角的两个面的法向量,由法向量夹角的余弦可得二面角的余弦.
中由得余弦定理可得余弦值.也可求出二面角的两个面的法向量,由法向量夹角的余弦可得二面角的余弦.
试题解析:
(Ⅰ)由![]() ,易知
,易知![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设![]() 点的坐标为
点的坐标为![]() ,则由
,则由![]() ,
,
可得![]()
![]() ,
,
解得![]() ,
,
所以![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,
则![]() ,
, ![]() ,
, ![]() 为二面角
为二面角![]() 的平面角.
的平面角.
由(Ⅰ)知,在![]() 中,
中, ![]() ,
, ![]() ,
,
则由余弦定理知![]() ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)对任意的
 ,
,  恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
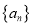 的首项为
的首项为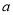 ,公差为
,公差为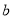 ,等比数列
,等比数列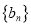 的首项为
的首项为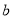 ,公比为
,公比为 .
. (Ⅰ)若数列
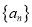 的前
的前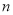 项和
项和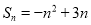 ,求
,求 ,
, 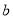 的值;
的值;(Ⅱ)若
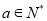 ,
, 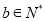 ,且
,且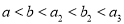 .
. (i)求
 的值;
的值;(ii)对于数列
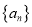 和
和 ,满足关系式
,满足关系式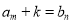 ,
, 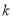 为常数,且
为常数,且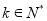 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量
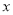 分布在
分布在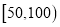 内,且销售量
内,且销售量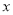 的分布频率
的分布频率 .
.(Ⅰ)求
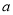 的值并估计销售量的平均数;
的值并估计销售量的平均数;(Ⅱ)若销售量大于等于70,则称该日畅销,其余为滞销.在畅销日中用分层抽样的方法随机抽取8天,再从这8天中随机抽取3天进行统计,设这3天来自
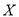 个组,求随机变量
个组,求随机变量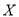 的分布列及数学期望(将频率视为概率).
的分布列及数学期望(将频率视为概率). -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系
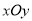 中,直线
中,直线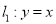 与直线
与直线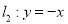 之间的阴影部分即为
之间的阴影部分即为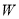 ,区域
,区域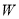 中动点
中动点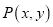 到
到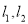 的距离之积为1.
的距离之积为1.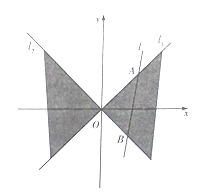
(Ⅰ)求点
 的轨迹
的轨迹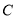 的方程;
的方程;(Ⅱ)动直线
 穿过区域
穿过区域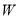 ,分别交直线
,分别交直线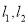 于
于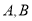 两点,若直线
两点,若直线 与轨迹
与轨迹 有且只有一个公共点,求证:
有且只有一个公共点,求证: 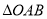 的面积恒为定值.
的面积恒为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
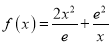 ,
,  ,其中
,其中 为自然对数的底数.
为自然对数的底数.(Ⅰ)讨论函数
 的单调性.
的单调性.(Ⅱ)是否存在实数
 ,使
,使 对任意
对任意 恒成立?若存在,试求出
恒成立?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量
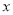 分布在
分布在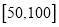 内,且销售量
内,且销售量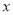 的分布频率
的分布频率 .
.(Ⅰ)求
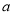 的值.
的值.(Ⅱ)若销售量大于等于80,则称该日畅销,其余为滞销,根据是否畅销从这50天中用分层抽样的方法随机抽取5天,再从这5天中随机抽取2天,求这2天中恰有1天是畅销日的概率(将频率视为概率).
相关试题

