【题目】已知函数f(x)=x3﹣3x.
(1)求曲线y=f(x)在点x=2处的切线方程;
(2)若过点A(1,m)(m≠﹣2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
参考答案:
【答案】
(1)解:f'(x)=3x2﹣3,f'(2)=9,f(2)=23﹣3×2=2
∴曲线y=f(x)在x=2处的切线方程为y﹣2=9(x﹣2),即9x﹣y﹣16=0
(2)解:过点A(1,m)向曲线y=f(x)作切线,设切点为(x0,y0)
则y0=x03﹣3x0,k=f'(x0)=3x02﹣3.
则切线方程为y﹣(x03﹣3x0)=(3x02﹣3)(x﹣x0)
将A(1,m)代入上式,整理得2x03﹣3x02+m+3=0.
∵过点A(1,m)(m≠﹣2)可作曲线y=f(x)的三条切线
∴方程2x3﹣3x2+m+3=0(*)有三个不同实数根、
记g(x)=2x3﹣3x2+m+3,g'(x)=6x2﹣6x=6x(x﹣1)、
令g'(x)=0,x=0或1
则x,g'(x),g(x)的变化情况如下表
x | (﹣∞,0) | 0 | (0,1) | 1 | (1,+∞) |
g'(x) | + | 0 | ﹣ | 0 | + |
g(x) | 递增 | 极大 | 递减 | 极小 | 递增 |
当x=0,g(x)有极大值m+3;x=1,g(x)有极小值m+2
由题意有,当且仅当 ![]() 即
即 ![]() 时,
时,
函数g(x)有三个不同零点、
此时过点A可作曲线y=f(x)的三条不同切线.故m的范围是(﹣3,﹣2)
【解析】(1)先求导数f'(x)=3x2﹣3,欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.(2)先将过点A(1,m)(m≠﹣2)可作曲线y=f(x)的三条切线转化为:方程2x3﹣3x2+m+3=0(*)有三个不同实数根,记g(x)=2x3﹣3x2+m+3,g'(x)=6x2﹣6x=6x(x﹣1),下面利用导数研究函数g(x)的零点,从而求得m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
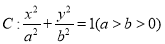 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为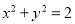 .
. (1)求椭圆
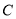 的方程;
的方程;(2)若抛物线
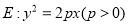 的焦点与椭圆
的焦点与椭圆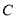 的一个焦点
的一个焦点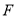 重合,直线
重合,直线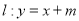 与抛物线
与抛物线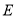 交于两点
交于两点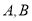 ,且
,且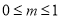 ,求
,求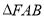 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取
 部进行测试,其结果如下:
部进行测试,其结果如下:甲种手机供电时间(小时)





乙种手机供电时间(小时)






(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述
 部乙种手机中随机抽取
部乙种手机中随机抽取 部,记所抽
部,记所抽 部手机供电时间不小于
部手机供电时间不小于 小时的个数为
小时的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点为极点O,
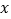 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为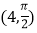 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型
木地板A
木地板B
木地板C
环保型
150
200
Z
普通型
250
400
600
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的离心率为
的离心率为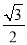 ,点
,点 ,
, 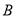 ,
,  分别为椭圆的右顶点、上顶点和右焦点,且
分别为椭圆的右顶点、上顶点和右焦点,且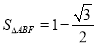 .
.(1)求椭圆
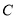 的方程;
的方程;(2)已知直线
 :
: 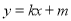 被圆
被圆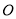 :
: 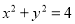 所截得的弦长为
所截得的弦长为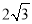 ,若直线
,若直线 与椭圆
与椭圆 交于
交于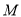 ,
, 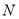 两点,求
两点,求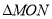 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是
 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中又放回的摸球,每次摸出一个,共摸5次 ①恰好有3次摸到红球的概率;
②第一次、第三次、第五次摸到红球的概率.
(2)若A、B两个袋子中的球之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是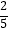 ,求p的值.
,求p的值.
相关试题

