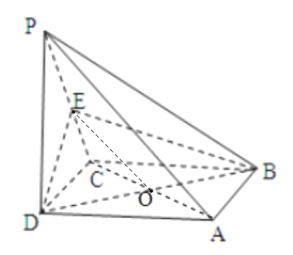
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧棱
是正方形,侧棱![]() 底面
底面![]() ,
,![]() 是
是![]() 的中点,求证:
的中点,求证:

(1)![]() 平面
平面![]() ;
;
(2)![]() .
.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接AC交BD于O,连接OE,由题意可证得OE∥PA,利用线面平行的判断定理可得PA∥平面EDB.
(2)由线面垂直的定义可得PD⊥AD,且AD⊥CD,据此可知AD⊥平面PCD,故AD⊥PC.
(1)连接AC交BD于O,连接OE,
∵底面ABCD是正方形,∴O为AC中点,
∵在△PAC中,E是PC的中点,
∴OE∥PA,
∵OE平面EDB,PA平面EDB,
∴PA∥平面EDB.
(2)∵侧棱PD⊥底面ABCD,AD底面ABCD,
∴PD⊥AD,
∵底面ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,
∴AD⊥平面PCD.
∴AD⊥PC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 ﹣k(
﹣k(  +lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
+lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆
 +
+  =1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,  =2
=2  ,△DF1F2的面积为
,△DF1F2的面积为  . (Ⅰ)求该椭圆的标准方程;
. (Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.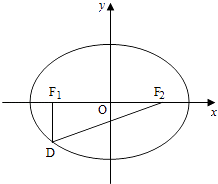
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(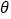 为参数);在极坐标系(与直角坐标系
为参数);在极坐标系(与直角坐标系 取相同的单位长度,且以原点
取相同的单位长度,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为 .
.(1)求曲线
 的普通方程和直线
的普通方程和直线 的直角坐标方程;
的直角坐标方程;(2)求直线
 被曲线
被曲线 截得的弦长.
截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学
不喜欢数学
总计
男
30
①
45
女
②
25
45
总计
③
④
90
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 :
: (
( 为参数),曲线
为参数),曲线 :
: (
( 为参数).
为参数).(1)设
 与
与 相交于
相交于 ,
, 两点,求
两点,求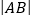 的值;
的值;(2)若把曲线
 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 ,纵坐标压缩为原来的
,纵坐标压缩为原来的 ,得到曲线
,得到曲线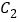 ,设点
,设点 是曲线
是曲线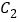 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系
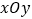 中,曲线
中,曲线 的方程是
的方程是 ,直线
,直线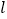 经过点
经过点 ,倾斜角为
,倾斜角为 ,以
,以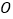 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)写出曲线
 的极坐标方程和直线
的极坐标方程和直线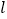 的参数方程;
的参数方程;(2)设直线
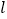 与曲线
与曲线 相交于
相交于 ,
,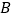 两点,求
两点,求 的值.
的值.
相关试题

