搜索
【题目】设命题p：（4x﹣3）2≤1；命题q：x2﹣（2a+1）x+a（a+1）≤0，若￢p是￢q的必要不充分条件，求实数a的取值范围．
参考答案：
【答案】解：设A={x|（4x﹣3）2≤1}，B={x|x2﹣（2a+1）x+a（a+1）≤0}，
易知A={x| 
≤x≤1}，B={x|a≤x≤a+1}．
由p是q的必要不充分条件，从而p是q的充分不必要条件，即AB，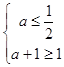
且两等号不能同时取．
故所求实数a的取值范围是[0， ]．
【解析】分别解出命题p和命题q中不等式的解集得到集合A和集合B，根据p是q的必要不充分条件，得到q是p的必要不充分条件，即q推不出p，而p能推出q．说明P的解集被q的解集包含，即集合A为集合B的真子集，列出关于a的不等式，求出不等式的解集即可得到a的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设不等式x2﹣2ax+a+2≤0的解集为M，若M[1，4]，求实数a的范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知集合A={x|x2+x+p=0}．
（Ⅰ）若A=，求实数p的取值范围；
（Ⅱ）若A中的元素均为负数，求实数p的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】将函数y=2cos（x﹣
）的图象上所有的点的横坐标缩短到原来的 
倍（纵坐标不变），得到函数y=g（x）的图象，则函数y=g（x）的图象（ ）
A.关于点（﹣
，0）对称
B.关于点（
，0）对称
C.关于直线x=﹣ 对称
D.关于直线x= 对称 -
科目： 来源： 题型：
查看答案和解析>>【题目】某校对高三年级的学生进行体检，现将高三男生的体重（单位：㎏）数据进行整理后分成五组，并绘制频率分布直方图（如图所示）．根据一般标准，高三男生的体重超过65㎏属于偏胖，低于55㎏属于偏瘦，已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25、0.20、0.10、0.05，第二小组的频率数为400，则该校高三年级的男生总数和体重正常的频率分别为（ ）
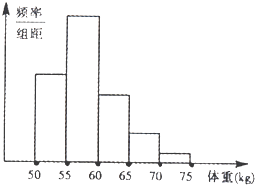
A.1000，0.50
B.800，0.50
C.1000，0.60
D.800，0.60 -
科目： 来源： 题型：
查看答案和解析>>【题目】记max{x，y}=
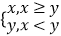，若f（x），g（x）均是定义在实数集R上的函数，定义函数h（x）=max{f（x），g（x）}，则下列命题正确的是（ ）
A.若f（x），g（x）都是单调函数，则h（x）也是单调函数
B.若f（x），g（x）都是奇函数，则h（x）也是奇函数
C.若f（x），g（x）都是偶函数，则h（x）也是偶函数
D.若f（x）是奇函数，g（x）是偶函数，则h（x）既不是奇函数，也不是偶函数 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
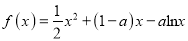.（Ⅰ）讨论
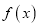的单调性；（Ⅱ）设
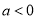，若对
， 
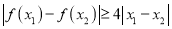，求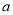
的取值范围.
相关试题
