【题目】设不等式x2﹣2ax+a+2≤0的解集为M,若M[1,4],求实数a的范围.
参考答案:
【答案】解:M[1,4]有两种情况:其一是M=,此时△<0;其二是M≠,此时△=0或△>0,
分三种情况计算a的取值范围.
设f (x)=x2﹣2ax+a+2,有△=(﹣2a)2﹣4(a+2)=4(a2﹣a﹣2).
(1)当△<0时,﹣1<a<2,M=[1,4].
(2)当△=0时,a=﹣1或2.
当a=﹣1时,M={﹣1}[1,4],故舍去.
当a=2时,M={2}[1,4].
(3)当△>0时,有a<﹣1或a>2.
设方程f (x)=0的两根为x1 , x2 , 且x1<x2 ,
那么M=[x1 , x2],由M[1,4]可得 1≤x1<x2≤4,故应有f(1)≥0,f(4)≥0,
且f (x)=0的对称轴x=a∈[1,4],即![]() ,
,
∴ ,解得2<a≤
,解得2<a≤![]() .
.
综上可得,M[1,4]时,a的取值范围是 (﹣1,![]() ].
].
【解析】M[1,4]有两种情况:其一是M=,此时△<0;其二是M≠,此时△=0或△>0,分三种情况计算a的取值范围,再取并集,即得所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
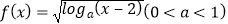 的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
的定义域为集合A,已知集合B={x|1<x<3},C={x|x≥m},全集为R.
(1)求(RA)∩B;
(2)若(A∪B)∩C≠,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某射击运动员每次射击击中目标的概率都为,现采用随机模拟的方法估计该运动员4次射击至少3次击中目标的概率:先由计算器产生0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,再以每4个随机数为一组,代表4次射击的结果,经随机模拟产生了如下20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
据此估计,该射击运动员4次射击至少3次击中目标的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合M={(x,y)|f(x,y)=0},若对任意P1(x1 , y1)∈M,均不存在P2(x2 , y2)∈M使得x1x2+y1y2=0成立,则称集合M为“好集合”,下列集合为“好集合”的是( )
A.M={(x,y)|y﹣lnx=0}
B.M={(x,y)|y﹣ x2﹣1=0}
x2﹣1=0}
C.M={(x,y)|(x﹣2)2+y2﹣2=0}
D.M={(x,y)|x2﹣2y2﹣1=0} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2+x+p=0}.
(Ⅰ)若A=,求实数p的取值范围;
(Ⅱ)若A中的元素均为负数,求实数p的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=2cos(x﹣
 )的图象上所有的点的横坐标缩短到原来的
)的图象上所有的点的横坐标缩短到原来的  倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
A.关于点(﹣ ,0)对称
,0)对称
B.关于点( ,0)对称
,0)对称
C.关于直线x=﹣ 对称
对称
D.关于直线x= 对称
对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:(4x﹣3)2≤1;命题q:x2﹣(2a+1)x+a(a+1)≤0,若¬p是¬q的必要不充分条件,求实数a的取值范围.
相关试题

