【题目】阅读下面的类比过程。
(1)在一维直线上,线段是一个封闭的中心对称图形,有命题1:不重合的两点决定一条线段;
(2)在二维平面上,圆是一个封闭的中心对称图形,有命题2:不共线的三点决定一个圆;
(3)在三维空间中,球是一个封闭的中心对称图形,类比猜想:不共面的四点决定一个球。
证明或否定这个类比猜想:不共面的四点决定一个球。
参考答案:
【答案】答案是肯定的
【解析】
由![]() 、
、![]() 、
、![]() 、
、![]() 四点不共面得
四点不共面得![]() 、
、![]() 、
、![]() 三点不共线,
三点不共线,
据命题2,![]() 、
、![]() 、
、![]() 三点可以决定一个圆,记圆心为
三点可以决定一个圆,记圆心为![]() ,并记
,并记![]() 、
、![]() 、
、![]() 决定的平面为
决定的平面为![]() ,
,
过![]() 作平面
作平面![]() 的垂线
的垂线![]() ,则直线
,则直线![]() 上每一点到
上每一点到![]() 、
、![]() 、
、![]() 的距离相等。
的距离相等。
联结![]() ,作平面
,作平面![]() 垂直平分线段
垂直平分线段![]() ,则平面
,则平面![]() 必与直线
必与直线![]() 相交,若不然,
相交,若不然,
无论是![]() 与平面
与平面![]() 平行,还是
平行,还是![]() 在平面
在平面![]() 上,都将得出
上,都将得出![]() ,但
,但![]() ,
,
故有![]() 或
或![]() ,这和
,这和![]() 与平面
与平面![]() 交于点
交于点![]() 矛盾,
矛盾,
所以,平面![]() 与直线
与直线![]() 相交,记交点为
相交,记交点为![]() ,则
,则![]() ,故以
,故以![]() 为球心,
为球心,![]() 为半径可以作一个球,且由球心、半径的唯一性知这个球是唯一的。
为半径可以作一个球,且由球心、半径的唯一性知这个球是唯一的。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆

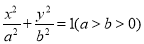 的右顶点
的右顶点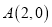 ,离心率为
,离心率为 ,
,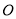 为坐标原点.
为坐标原点.(Ⅰ)求椭圆
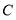 的方程;
的方程;(Ⅱ)已知
 (异于点
(异于点 )为椭圆
)为椭圆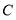 上一个动点,过
上一个动点,过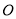 作线段
作线段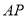 的垂线
的垂线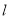 交椭圆
交椭圆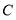 于点
于点 ,求
,求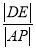 的取值范围.
的取值范围.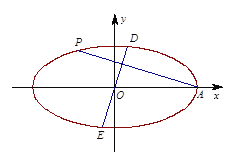
-
科目: 来源: 题型:
查看答案和解析>>【题目】以
 为直径的圆上每一点都染上了红、黄、蓝三色之一,已知
为直径的圆上每一点都染上了红、黄、蓝三色之一,已知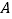 、
、 染上了红色,联结圆上的点组成三角形,给出4个结论:
染上了红色,联结圆上的点组成三角形,给出4个结论:①必定存在一个直角三角形,三个顶点同为红色;
②必定存在一个直角三角形,三个顶点同色;
③必定存在一个直角三角形,三个顶点全不同色;
④必定存在一个直角三角形,或都三个顶点同色,或者三个顶点全不同色。
则真命题的个数是( )个。
A. 1 B. 2
C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一道题目的证明,指出其中的一处错误。题目:平面上有六个点,任何三点都是三边互不相等三角形的顶点,则这些三角形中有一个的最短边又是另一个三角形的最长边。证明:第一步,对已知的六个点作两两连线,可以得出15条边,记为
 ,
, ,…,
,…, .第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设
.第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设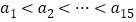 .第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则
.第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则 、
、 、
、 组成的三角形的最长边
组成的三角形的最长边 ,也是
,也是 、
、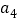 、
、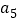 组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
 、
、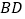 交于点
交于点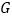 ,在
,在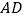 的延长线上任取一点
的延长线上任取一点 ,得凸四边形
,得凸四边形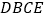 ,求证:
,求证: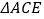 、
、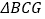 、
、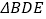 的外接圆三圆共点。
的外接圆三圆共点。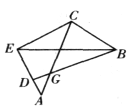
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
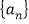 的前
的前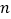 项和为
项和为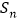 ,
,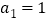 且
且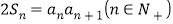 。
。(1)证明:
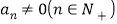 ,并求
,并求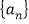 的通项公式;
的通项公式;(2)构造数列
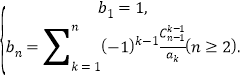 求证:无论给定多么大的正整数
求证:无论给定多么大的正整数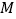 ,都必定存在一个
,都必定存在一个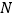 ,使
,使 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中, 是正三角形,四边形
是正三角形,四边形 是菱形,点
是菱形,点 是
是 的中点.
的中点.
(I)求证:
 // 平面
// 平面 ;
;(II)若平面
 平面
平面 ,
, , 求直线
, 求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
相关试题

